

Journal of Geographical Sciences >
Identifying the most important spatially distributed variables for explaining land use patterns in a rural lowland catchment in Germany
|
Chaogui Lei, M.Sc, E-mail: cglei@hydrology.uni-kiel.de |
Received date: 2018-11-08
Accepted date: 2019-02-21
Online published: 2019-12-05
Copyright
Land use patterns arise from interactive processes between the physical environment and anthropogenic activities. While land use patterns and the associated explanatory variables have often been analyzed on the large scale, this study aims to determine the most important variables for explaining land use patterns in the 50 km² catchment of the Kielstau, Germany, which is dominated by agricultural land use. A set of spatially distributed variables including topography, soil properties, socioeconomic variables, and landscape indices are exploited to set up logistic regression models for the land use map of 2017 with detailed agricultural classes. Spatial validation indicates a reasonable performance as the relative operating characteristic (ROC) ranges between 0.73 and 0.97 for all land use classes except for corn (ROC = 0.68). The robustness of the models in time is confirmed by the temporal validation for which the ROC values are on the same level (maximum deviation 0.1). Non-agricultural land use is generally better explained than agricultural land use. The most important variables are the share of drained area, distance to protected areas, population density, and patch fractal dimension. These variables can either be linked to agriculture or the river course of the Kielstau.
Chaogui LEI , Paul D. WAGNER , Nicola FOHRER . Identifying the most important spatially distributed variables for explaining land use patterns in a rural lowland catchment in Germany[J]. Journal of Geographical Sciences, 2019 , 29(11) : 1788 -1806 . DOI: 10.1007/s11442-019-1690-2
Figure 1 Location of the Kielstau catchment, spatial distribution of topography (LVA, 1992-2004), soil (BGR, 1999), main stream network (LANU, 2003), biogas plants, and land use in 2013 and 2017 |
Table 1 Areal percentages of land use classes in the Kielstau catchment in 2013 and 2017 |
| Settlement areas | Fallow | Grassland /Pasture | Corn | Other crops | Forest | Winter rye | Winter rape | Orchard /Garden | Winter wheat | Other cereals | Field bean | Winter barley | Water | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2013 | 10.5 | 0.7 | 20.8 | 13.0 | 1.6 | 3.1 | 1.4 | 10.8 | 0.5 | 22.0 | 1.2 | 1.0 | 11.8 | 1.8 |
| 2017 | 10.6 | 0.6 | 20.3 | 10.7 | 2.1 | 3.1 | 3.5 | 11.8 | 0.5 | 21.4 | 2.0 | 2.4 | 9.2 | 1.8 |
| Change | 0.1 | -0.1 | -0.5 | -2.3 | 0.5 | 0 | 2.1 | 1.0 | 0 | -0.6 | 0.8 | 1.4 | -2.6 | 0 |
Figure 2 Examples of potentially important explanatory variables to land use distribution |
Table 2 Spatially distributed explanatory variables used in this study |
| Variable | Unit | Source |
|---|---|---|
| Elevation | m | DEM for S.-H. (LVA, 1992-2004) |
| Aspect | Degree | Calculated from DEM |
| Slope | Degree | Calculated from DEM |
| Clay content | % | Digital soil map (BGR, 1999) |
| Silt content | % | |
| Sand content | % | |
| Rock content | % | |
| Organic carbon content | % | |
| Available water capacity | mm/mm | |
| Soil depth | mm | |
| Moist bulk density | mg/m3 | |
| Saturated hydraulic conductivity | mm/hr | |
| Moist soil albedo | - | |
| USLE K factor | - | |
| Drained soil share | % | |
| Distance to rivers | m | Calculated from river network shapefile (LANU, 2003) |
| Distance to roads | m | Calculated from road distribution derived from 2013, 2017 land use maps |
| Distance to villages | m | Calculated from village distribution derived from 2013, 2017 land use maps |
| Distance to protected areas | m | Calculated from distribution of protected areas (StiftungNaturschutz, 2016) |
| Distance to biogas plants | m | Calculated from biogas plants location |
| Population density | Persons/km2 | Calculated from community population and village distribution from 2013, 2017 land use maps |
| Patch size | m2 | Calculated from 2013 and 2017 land use maps |
| Patch perimeter | m | |
| Shape index | - | |
| Perimeter-area ratio | m-1 | |
| Fractal dimension | - |
Table 3 Best logistic regression models for each land use class: odds ratios for the explanatory variables and performance of each model as indicated by the relative operating characteristic (ROC) statistic for calibration, spatial and temporal validation. |
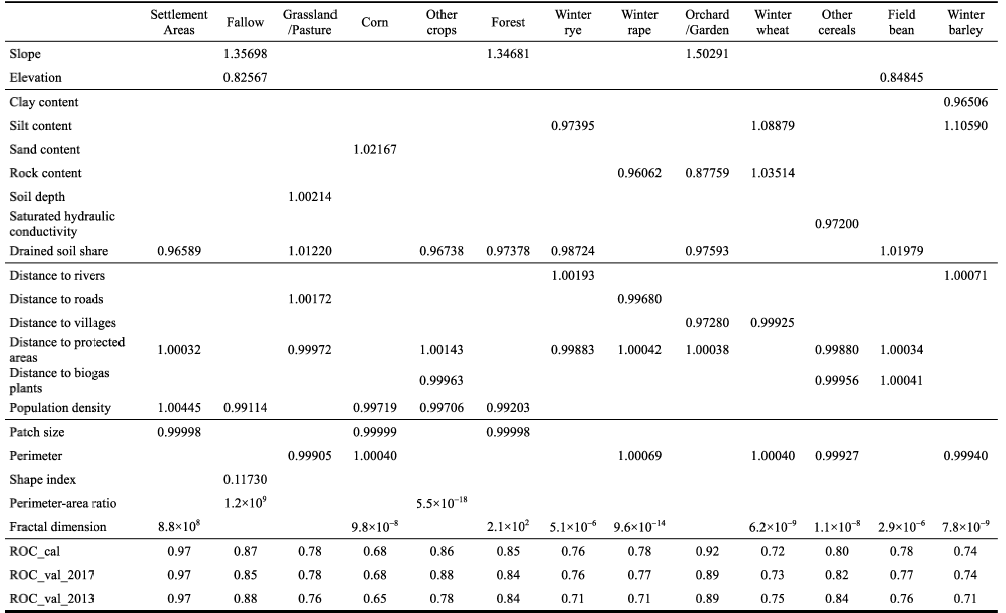 |
Table 4 Percentages of explanatory variables included into the 50 best logistic regression models for each land use class. The best model is marked in bold. |
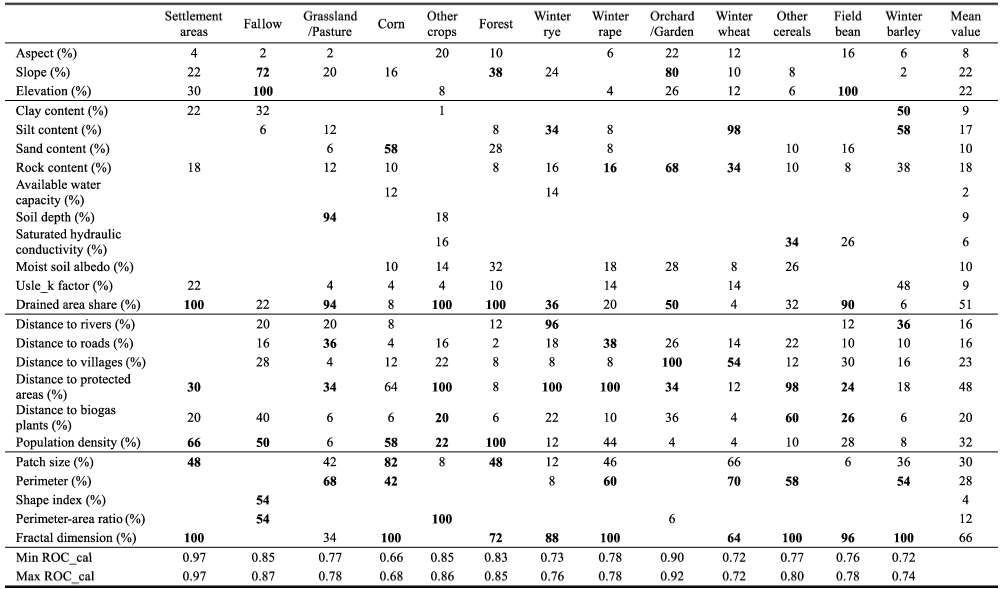 |
Figure 3 Probability maps for predicting each land use class pattern in 2013 using the best logistic regression models. The corresponding relative operating characteristic (ROC) statistic is provided. |
Figure 4 R-G-B composites indicating spatial competition among land use classes. Water areas are masked in white |
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
BGR, 1999. BUK 200, Bodenubersichtskarte 1:200 000. Bundesanstalt für Geowissenschaften und Rohstoffe: CC.1518 Flensburg, Hannover.
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
DWD, 2009. Weather and Climate Data from the German Weather Service., Offenbach, Station Flensburg 1957-2006 and Station Meierwik, 1993-2008, 1993-2008 ed, Offenbach.
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
LANU, 2003. LANDESAMT FÜR NATUR UND UMWELT SCHLESWIG-HOLSTEIN: Ausschnitt aus dem Basisgewässernetz des Landes Schleswig-Holstein für das Einzugsgebiet der Treene bis Treia. (Arc-View- Shape), Flintbek.
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
LVA, 1992-2004. DEM 25 m Grid Size, DEM 5 m Grid Size Derived from Topographic Maps 1:5 000 and Map of Schleswig-Holstein. Land survey office Schleswig-Holstein: Kiel.
|
| [38] |
LVA, 2013, 2016. ATKIS®-Digitale Orthophotos (DOP) with a ground resolution of 20 cm. Land Survey Office Schleswig-Holstein.
|
| [39] |
LVA, 2016. ATKIS® Digitales Basis-Landschaftsmodell (Basis-DLM). Land Survey Office Schleswig-Holstein: Kiel.
|
| [40] |
LVERMA-SH, Vermessungs-und Katasterverwaltung Schleswig-Holstein, 2004. Automatisierte Liegenschaftskarte (ALK).
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
|
| [47] |
|
| [48] |
|
| [49] |
|
| [50] |
|
| [51] |
|
| [52] |
|
| [53] |
|
| [54] |
|
| [55] |
|
| [56] |
|
| [57] |
|
| [58] |
|
| [59] |
|
| [60] |
|
| [61] |
|
| [62] |
|
| [63] |
|
| [64] |
StiftungNaturschutz, 2016. Flächenmanagement Kreis SL-Stiftung Naturschutz Schleswig-Holstein.
|
| [65] |
|
| [66] |
|
| [67] |
|
| [68] |
|
| [69] |
|
| [70] |
|
| [71] |
|
| [72] |
|
| [73] |
|
| [74] |
|
| [75] |
|
| [76] |
|
/
| 〈 |
|
〉 |