

Journal of Geographical Sciences >
Automatic mapping of lunar landforms using DEM-derived geomorphometric parameters
Author: Wang Jiao (1990-), PhD, specialized in planetary geomorphology and spatial analysis. E-mail: wjiao@lreis.ac.cn
Received date: 2017-06-13
Accepted date: 2017-07-31
Online published: 2017-09-07
Supported by
National Natural Science Foundation of China, No.41571388
National Special Basic Research Fund, No.2015FY210500
Copyright
Developing approaches to automate the analysis of the massive amounts of data sent back from the Moon will generate significant benefits for the field of lunar geomorphology. In this paper, we outline an automated method for mapping lunar landforms that is based on digital terrain analysis. An iterative self-organizing (ISO) cluster unsupervised classification enables the automatic mapping of landforms via a series of input raster bands that utilize six geomorphometric parameters. These parameters divide landforms into a number of spatially extended, topographically homogeneous segments that exhibit similar terrain attributes and neighborhood properties. To illustrate the applicability of our approach, we apply it to three representative test sites on the Moon, automatically presenting our results as a thematic landform map. We also quantitatively evaluated this approach using a series of confusion matrices, achieving overall accuracies as high as 83.34% and Kappa coefficients (K) as high as 0.77. An immediate version of our algorithm can also be applied for automatically mapping large-scale lunar landforms and for the quantitative comparison of lunar surface morphologies.
WANG Jiao , CHENG Weiming , ZHOU Chenghu , ZHENG Xinqi . Automatic mapping of lunar landforms using DEM-derived geomorphometric parameters[J]. Journal of Geographical Sciences, 2017 , 27(11) : 1413 -1427 . DOI: 10.1007/s11442-017-1443-z
Figure 1 Map showing the locations of our study areas as well as the positions of selected craters |
Figure 2 Flow chart illustrating the computational landform classification process applied in this study |
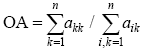
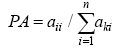
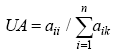
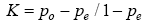
Figure 3 Dendrogram showing the relationships between the 20 landform classes generated by automatic classification within the LQ-8, LQ-11, and LQ-20 test areas. The gray rectangles denote the five major landform types identified manually by assigning geomorphologic interpretations to classes, while the multidimensional distance along the top of the dendrogram is the distance between classes in attribute space. |
Figure 4 Thematic map showing automatically identified landforms within the LQ-8 test area. The geographic categories corresponding with numbered landform classes are outlined in the legend |
Table 1 Average values for landform class morphologic parameters within the LQ-8 test area |
| Class | Count (pixels) | Elevation (m) | Filled elevation (m) | Slope (degree) | Filled slope (degree) | Relief (m) | Filled relief (m) |
|---|---|---|---|---|---|---|---|
| 1 | 106,694 | -697 | 5787 | 6.17 | 6.17 | 1188 | 1187 |
| 2 | 262,266 | 512 | 4579 | 6.54 | 6.54 | 1245 | 1244 |
| 3 | 304,078 | 1216 | 3877 | 6.58 | 6.6 | 1262 | 1261 |
| 4 | 288,478 | 1794 | 3301 | 6.63 | 6.63 | 1263 | 1262 |
| 5 | 249,714 | 2257 | 2839 | 6.67 | 6.67 | 1270 | 1272 |
| 6 | 239,441 | 2618 | 2482 | 6.75 | 6.74 | 1272 | 1273 |
| 7 | 229,001 | 2890 | 2215 | 6.78 | 6.79 | 1275 | 1276 |
| 8 | 229,510 | 3112 | 2004 | 6.8 | 6.8 | 1278 | 1278 |
| 9 | 222,440 | 3306 | 1796 | 6.9 | 6.9 | 1291 | 1291 |
| 10 | 238,691 | 3491 | 1608 | 6.98 | 6.99 | 1297 | 1297 |
| 11 | 253,876 | 3676 | 1423 | 6.99 | 6.99 | 1306 | 1306 |
| 12 | 258,172 | 3864 | 1237 | 7.00 | 7.00 | 1314 | 1313 |
| 13 | 261,774 | 4062 | 1040 | 7.02 | 7.02 | 1318 | 1318 |
| 14 | 263,442 | 4281 | 821 | 7.03 | 7.03 | 1325 | 1325 |
| 15 | 281,458 | 4539 | 562 | 7.03 | 7.03 | 1325 | 1325 |
| 16 | 308,016 | 4864 | 235 | 7.04 | 7.04 | 1336 | 1336 |
| 17 | 325,804 | 5280 | -182 | 7.24 | 7.25 | 1346 | 1346 |
| 18 | 316,858 | 5823 | -723 | 7.31 | 7.32 | 1396 | 1395 |
| 19 | 224,284 | 6548 | -1443 | 7.55 | 7.55 | 1412 | 1414 |
| 20 | 102,783 | 7743 | -2634 | 7.74 | 7.75 | 1472 | 1472 |
Table 2 Average values for landform class morphologic parameters within the LQ-11 test area |
| Class | Count (pixels) | Elevation (m) | Filled elevation (m) | Slope (degree) | Filled slope (degree) | Relief (m) | Filled relief (m) |
|---|---|---|---|---|---|---|---|
| 1 | 42,808 | -3569 | 8776 | 1.85 | 1.86 | 337 | 337 |
| 2 | 265,504 | -2766 | 7961 | 1.89 | 1.9 | 338 | 338 |
| 3 | 330,694 | -2516 | 7709 | 1.91 | 1.91 | 342 | 341 |
| 4 | 313,714 | -2306 | 7500 | 1.93 | 1.93 | 343 | 343 |
| 5 | 256,718 | -2139 | 7334 | 1.93 | 1.93 | 344 | 345 |
| 6 | 192,104 | -1996 | 7201 | 1.97 | 1.97 | 351 | 351 |
| 7 | 158,366 | -1898 | 7091 | 1.99 | 1.99 | 352 | 352 |
| 8 | 156,600 | -1808 | 6997 | 2.01 | 2.01 | 354 | 354 |
| 9 | 191,501 | -1732 | 6921 | 2.01 | 2.01 | 358 | 358 |
| 10 | 228,543 | -1662 | 6852 | 2.08 | 2.08 | 371 | 371 |
| 11 | 274,974 | -1594 | 6787 | 2.2 | 2.18 | 383 | 383 |
| 12 | 320,671 | -1528 | 6723 | 2.22 | 2.22 | 386 | 384 |
| 13 | 368,498 | -1461 | 6656 | 2.23 | 2.23 | 398 | 398 |
| 14 | 414,463 | -1389 | 6584 | 2.28 | 2.28 | 407 | 407 |
| 15 | 433,738 | -1303 | 6497 | 2.62 | 2.62 | 455 | 455 |
| 16 | 411,237 | -1184 | 6379 | 3.66 | 3.65 | 622 | 621 |
| 17 | 295,272 | -999 | 6194 | 4.97 | 4.96 | 847 | 847 |
| 18 | 185,843 | -680 | 5875 | 5.53 | 5.56 | 1116 | 1126 |
| 19 | 86,950 | -152 | 5349 | 6.75 | 6.74 | 1248 | 1247 |
| 20 | 38,582 | 856 | 4344 | 7.95 | 7.95 | 1485 | 1484 |
Figure 5 Thematic map showing automatically identified landforms within the LQ-11 test area. The geographic categories corresponding with numbered landform classes are outlined in the legend |
Table 3 Average values for landform class morphologic parameters within the LQ-20 test area |
| Class | Count (pixels) | Elevation (m) | Filled elevation (m) | Slope (degree) | Filled slope (degree) | Relief (m) | Filled relief (m) |
|---|---|---|---|---|---|---|---|
| 1 | 13,103,851 | -5184 | -184 | 6.84 | 6.84 | 272 | 287 |
| 2 | 7,767,995 | -3749 | 1251 | 10.49 | 10.49 | 432 | 447 |
| 3 | 3,022,547 | -3047 | 1953 | 10.92 | 10.92 | 460 | 481 |
| 4 | 3,932,609 | -2584 | 2416 | 11.37 | 11.37 | 478 | 522 |
| 5 | 2,662,286 | -2132 | 2868 | 12.70 | 12.70 | 540 | 668 |
| 6 | 2,023,806 | -1779 | 3221 | 14.08 | 14.08 | 603 | 955 |
| 7 | 2,486,296 | -1439 | 3561 | 13.53 | 13.53 | 581 | 1392 |
| 8 | 2,215,210 | -1115 | 3885 | 13.47 | 13.44 | 581 | 2684 |
| 9 | 2,665,493 | -821 | 2558 | 12.43 | 28.63 | 528 | 5942 |
| 10 | 3,546,739 | -543 | -3558 | 11.34 | 12.90 | 471 | 3494 |
| 11 | 4,014,407 | -276 | -3276 | 11.39 | 11.35 | 470 | 1489 |
| 12 | 4,133,915 | -9 | -3009 | 11.75 | 11.75 | 483 | 948 |
| 13 | 4,717,575 | 277 | -2723 | 12.33 | 12.33 | 509 | 724 |
| 14 | 5,023,863 | 606 | -2394 | 13.51 | 13.51 | 560 | 666 |
| 15 | 5,161,705 | 1012 | -1988 | 14.22 | 14.22 | 593 | 646 |
| 16 | 5,667,975 | 1514 | -1486 | 14.74 | 14.74 | 618 | 651 |
| 17 | 5,556,587 | 2166 | -834 | 15.04 | 15.04 | 635 | 662 |
| 18 | 5,911,671 | 3045 | 45 | 15.28 | 15.28 | 650 | 678 |
| 19 | 3,473,170 | 4427 | 1427 | 16.50 | 16.50 | 707 | 748 |
| 20 | 1,368,136 | 6032 | 3032 | 16.74 | 16.74 | 722 | 762 |
Figure 6 Thematic map to show automatically identified landforms within the LQ-20 test area. The geographic categories corresponding with numbered landform classes are outlined in the legend |
Table 4 Error matrix for the best classification result |
| Test area | Landform | UA% | PA% | OA% | K |
|---|---|---|---|---|---|
| LQ-8 | Crater | 70.98 | 87.72 | 76.04 | 0.68 |
| Mare | - | - | |||
| Lowland | 86.4 | 85.1 | |||
| Highrelief | 85.41 | 56.79 | |||
| Highland | 64.24 | 81.72 | |||
| LQ-11 | Crater | 61.53 | 97.45 | 83.34 | 0.77 |
| Mare | 85.04 | 82.95 | |||
| Lowland | 94.97 | 88.35 | |||
| Highrelief | 81.77 | 71.02 | |||
| Highland | - | - | |||
| LQ-20 | Crater | 78.30 | 85.93 | 70.12 | 0.59 |
| Mare | 92.26 | 69.01 | |||
| Lowland | 77.54 | 68.62 | |||
| Highrelief | 53.31 | 67.24 | |||
| Highland | 76.09 | 87.81 |
Figure 7 Local views of Crater A and Crater B (a), as well as Crater C, Crater D, and Crater E (b). Topographic contours have been superimposed onto landform maps in both cases; geographic categories corresponding with numbered landform classes are outlined in the legend |
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
/
| 〈 |
|
〉 |