

Journal of Geographical Sciences >
Quality control and homogenization of daily meteorological data in the trans-boundary region of the Jhelum River basin
Author: Rashid Mahmood, E-mail: rashi1254@gmail.com; Jia Shaofeng, E-mail: jiasf@igsnrr.ac.cn
Received date: 2015-07-22
Accepted date: 2015-10-29
Online published: 2016-12-20
Supported by
National Natural Sciences Foundation of China, No.41471463
President’s International Fellowship Initiative CAS
Copyright
Many studies such as climate variability, climate change, trend analysis, hydrological designs, agriculture decision-making etc. require long-term homogeneous datasets. Since homogeneous climate data is not available for climate analysis in Pakistan and India, the present study emphases on an extensive quality control and homogenization of daily maximum temperature, minimum temperature and precipitation data in the Jhelum River basin, Pakistan and India. A combination of different quality control methods and relative homogeneity tests were applied to achieve the objective of the study. To check the improvement after homogenization, correlation coefficients between the test and reference series calculated before and after the homogenization process were compared with each other. It was found that about 0.59%, 0.78% and 0.023% of the total data values are detected as outliers in maximum temperature, minimum temperature and precipitation data, respectively. About 32% of maximum temperature, 50% of minimum temperature and 7% of precipitation time series were inhomogeneous, in the Jhelum River basin. After the quality control and homogenization, 1% to 11% improvement was observed in the infected climate variables. This study concludes that precipitation daily time series are fairly homogeneous, except two stations (Naran and Gulmarg), and of a good quality. However, maximum and minimum temperature datasets require an extensive quality control and homogeneity check before using them into climate analysis in the Jhelum River basin.
Rashid MAHMOOD , JIA Shaofeng . Quality control and homogenization of daily meteorological data in the trans-boundary region of the Jhelum River basin[J]. Journal of Geographical Sciences, 2016 , 26(12) : 1661 -1674 . DOI: 10.1007/s11442-016-1351-7
Figure 1 Location of the study area and geographic distribution of weather stations |
Table 1 Geographic and basic information about the climate stations available in the Jhelum River basin |
 |
Table 2 Local extremes of Tx, Tn and Pr |
| Variable | High Extreme | Low Extreme | Source |
|---|---|---|---|
| Tx (°C) | 53.5 | -24.1 | (PMD, 2014; Atta Ur and Shaw, 2015) |
| Tn (°C) | 53.5 | -24.1 | |
| Pr (mm) | 668 | - | (PMD, 2014) |
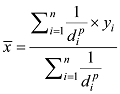
 is the reference series; yi neighbor station; d is the distance between the test and neighbor stations; n is the number of neighbor stations; p is the power of distance—the higher the value of p, the greater the weights for the nearest neighbor station. In this study, a power of 0.5 and 1, as recommended in the manual of ProclimDB (Processing of Climatological Database) software (Štěpánek, 2010), was used to create reference series for temperature (Tx and Tn) and precipitation, respectively.
is the reference series; yi neighbor station; d is the distance between the test and neighbor stations; n is the number of neighbor stations; p is the power of distance—the higher the value of p, the greater the weights for the nearest neighbor station. In this study, a power of 0.5 and 1, as recommended in the manual of ProclimDB (Processing of Climatological Database) software (Štěpánek, 2010), was used to create reference series for temperature (Tx and Tn) and precipitation, respectively.Figure 2 Average correlation coefficients between weather stations in the Jhelum River basin |
Figure 3 Variation in correlation coefficients with respect to distance between weather stations in the Jhelum River basin |
Table 3 Percentages of erroneous data in Tx, Tn and Pr time series during quality control in the Jhelum River basin |
| Method | Tx (%) | Tn (%) | Pr (%) | |
|---|---|---|---|---|
| Total number of values processed | 319100 | 315794 | 418499 | |
| High/Low extremes | 0.0019 | 0.0076 | 0.0010 | |
| Internal consistency | Tx lower than Tn | 0.0279 | 0.0279 | ‒ |
| Flat-liner | 0.0677 | 0.0874 | 0.0000 | |
| Excessive diurnal temperature range | 0.0000 | 0.0000 | ‒ | |
| Temporal outliers | 0.2407 | 0.2825 | ‒ | |
| Spatial outliers | 0.2288 | 0.3467 | 0.0222 | |
| Total | 0.5669 | 0.7521 | 0.0232 | |
Table 4 Inhomogeneous stations and number of breakpoints in Tx, Tn and Pr in the Jhelum River basin |
| SR | Station | Year of inhomogeneities | ||
|---|---|---|---|---|
| Tx | Tn | Pr | ||
| 1 | Bagh | 1970 | 1970, 2004 | |
| 2 | Balakot | 1979 | ||
| 3 | Dhudial | 1989 | 1989 | |
| 4 | Domel | 1969, 1989 | 1969 | |
| 5 | Gulmarg | 1987 | 1968 | |
| 6 | Gharidopatta | 1969 | ||
| 7 | Kotli | 1981, 1995 | 1970 | |
| 8 | Kupwara | 1985 | ||
| 9 | Mangla | 1972 | ||
| 10 | Murree | 1989 | 1989 | |
| 11 | Muzaffarabad | 1969 | 1969 | |
| 12 | Naran | 1989 | 1988 | |
| 13 | Rawalakot | 1990 | ||
| Stations having inhomogeneities | 7 | 11 | 2 | |
| Stations having inhomogeneities (%) | 31.8 | 50.0 | 7.4 | |
Figure 4 Detected inhomogeneities (a) in Tx on Gharidopatta weather station, (b) in Tn on Rawalakot and (c) in Pr on Naran, in the Jhelum River basin |
Figure 5 Daily adjustments for the identified breakpoint in 1990 in Tn of Rawalakot station (shown in Figure 4b) |
Figure 6 Change in correlation coefficients (CC) between test and reference series before and after homogenization |
The authors have declared that no competing interests exist.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
PMD, cited 2015: Extreme Events Reports. [Available online at cited 2015.]
|
| 23 |
|
| 24 |
|
| 25 |
Štěpánek P, cited 2015: ProClimDB - Software for Processing Climatological Datasets. Available online at cited 2015.
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
/
| 〈 |
|
〉 |