

Journal of Geographical Sciences >
A novel method for approximating intercity networks: An empirical comparison for validating the city networks in two Chinese city-regions
*Corresponding author: Wu Kang (1985-), PhD and Assistant Professor, specialized in urban economic geography and planning. E-mail:wukang@cueb.edu.cn
Author: Zhao Miaoxi (1979-), PhD and Associate Professor, national registered urban planner, specialized in urban and regional planning. E-mail:zmx0207@163.com
Received date: 2014-03-17
Accepted date: 2014-04-02
Online published: 2015-03-15
Supported by
National Natural Science Foundation of China, No.51478189;No.41401178
National Social Science Fund, 11&ZD154
State Key Laboratory of Subtropical Building Science, No.2013KB20
Fundamental Research Funds for the Central Universities, No.2013ZZ0022
Copyright
A network perspective has increasingly become an organizational paradigm for understanding regional spatial structures. Based on a critical overview of existing empirical models for estimating intercity networks based on firm linkages, this study extends the recently proposed regional corporate city model algorithm by proposing a new method for approximating urban networks based on the locational strategies of firms. The new method considers both regional and hierarchical network features and avoids the information loss associated with the conversion from two-mode firm-city networks to one-mode city-city networks. In addition, networks estimated by using the method proposed herein are suitable when employing social network analysis. Finally, this method is empirically validated by examining intercity firm networks formed by advanced producer services firms in China’s two largest metropolitan areas, namely the Yangtze River Delta and Pearl River Delta. The presented empirical analysis suggests two main findings. First, in contrast to conventional methods (e.g., the interlocking city network model), our new method produces regional and hierarchical urban networks that more closely resemble reality. Second, the new method allows us to use social network analysis to assess betweenness and closeness centralities. However, regardless of the model applied, the validity of any method that measures urban networks depends on the soundness of its underlying assumptions about how network actors (firms, in our case) interact.
ZHAO Miaoxi , WU Kang , LIU Xingjian , BEN Derudder . A novel method for approximating intercity networks: An empirical comparison for validating the city networks in two Chinese city-regions[J]. Journal of Geographical Sciences, 2015 , 25(3) : 337 -354 . DOI: 10.1007/s11442-015-1172-0
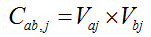
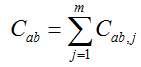

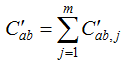
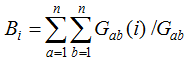
Figure 1 Overlaying process of firms’ networks in cities |
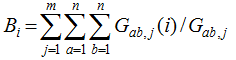
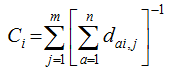
Figure 2 APS networks for the YRD and PRD based on the IWCNM (a) and RCCM (b) |
Table 1 Network matrix based on the IWCNM |
| Shanghai | Nanjing | Suzhou | Wuxi | Hangzhou | Ningbo | Guangzhou | Shenzhen | Dongguan | Foshan | |
|---|---|---|---|---|---|---|---|---|---|---|
| Shanghai | 576 | 374 | 222 | 677 | 336 | 1153 | 1046 | 161 | 165 | |
| Nanjing | 576 | 264 | 180 | 416 | 225 | 387 | 505 | 125 | 138 | |
| Suzhou | 374 | 264 | 123 | 243 | 163 | 266 | 305 | 94 | 77 | |
| Wuxi | 222 | 180 | 123 | 163 | 132 | 177 | 207 | 97 | 90 | |
| Hangzhou | 677 | 416 | 243 | 163 | 260 | 482 | 563 | 133 | 134 | |
| Ningbo | 336 | 225 | 163 | 132 | 260 | 255 | 277 | 115 | 119 | |
| Guangzhou | 1153 | 387 | 266 | 177 | 482 | 255 | 720 | 168 | 159 | |
| Shenzhen | 1046 | 505 | 305 | 207 | 563 | 277 | 720 | 186 | 178 | |
| Dongguan | 161 | 125 | 94 | 97 | 133 | 115 | 168 | 186 | 101 | |
| Foshan | 165 | 138 | 77 | 90 | 134 | 119 | 159 | 178 | 101 |
Table 2 Network matrix based on the RCCM |
| Shanghai | Nanjing | Suzhou | Wuxi | Hangzhou | Ningbo | Guang- zhou | Shen- zhen | Dong- guan | Foshan | |
|---|---|---|---|---|---|---|---|---|---|---|
| Shanghai | 4 | 1 | 3 | 2 | 1 | 6 | 22 | 1 | 0 | |
| Nanjing | 20 | 1 | 2 | 1 | 0 | 2 | 14 | 1 | 0 | |
| Suzhou | 19 | 8 | 2 | 3 | 3 | 0 | 7 | 0 | 0 | |
| Wuxi | 16 | 10 | 5 | 9 | 6 | 3 | 11 | 1 | 0 | |
| Hangzhou | 25 | 3 | 1 | 2 | 1 | 3 | 14 | 1 | 0 | |
| Ningbo | 14 | 3 | 1 | 0 | 3 | 2 | 8 | 0 | 0 | |
| Guangzhou | 23 | 3 | 0 | 2 | 1 | 0 | 17 | 0 | 0 | |
| Shenzhen | 23 | 4 | 1 | 2 | 2 | 0 | 6 | 1 | 0 | |
| Dongguan | 5 | 0 | 1 | 0 | 0 | 0 | 12 | 15 | 0 | |
| Foshan | 5 | 0 | 0 | 0 | 0 | 0 | 13 | 17 | 2 |
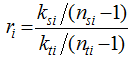
Table 3 Ratios of intra-regional links based on the IWCNM and RCCM |
| YRD | PRD | ||||
|---|---|---|---|---|---|
| City | IWCNM | RCCM | City | IWCNM | RCCM |
| Shanghai | 0.812 | 1.214 | Guangzhou | 0.793 | 1.988 |
| Nanjing | 0.988 | 1.475 | Shenzhen | 0.797 | 1.559 |
| Zhenjiang | 1.086 | 1.562 | Dongguan | 1.004 | 2.311 |
| Suzhou | 1.032 | 1.559 | Zhuhai | 1.068 | 2.240 |
| Nantong | 1.086 | 1.562 | Foshan | 0.995 | 2.453 |
| Yangzhou | 1.066 | 1.562 | Zhaoqing | 1.006 | 2.667 |
| Changzhou | 1.092 | 1.563 | Shan | 0.964 | 2.533 |
| Wuxi | 1.038 | 1.502 | Jiangmen | 1.006 | 2.667 |
| Taizhou (Jiangsu) | 1.071 | 1.562 | Huizhou | 1.035 | 2.667 |
| Hangzhou | 0.956 | 1.485 | |||
| Huzhou | 1.031 | 1.560 | |||
| Jiangxing | 1.071 | 1.562 | |||
| Ningbo | 0.998 | 1.514 | |||
| Shaoxing | 1.071 | 1.561 | |||
| Taizhou (Zhejiang) | 1.055 | 1.562 | |||
| Average | 1.030 | 0.963 | Average | 1.520 | 2.343 |
Table 4 Independent sample test of the ratio of the intra-regional links for the YRD and PRD |
| Calculation model | Variance | Levene test for equality | t-test for equality | |||
|---|---|---|---|---|---|---|
| F | Sig. | t | df | Sig. (2-tailed) | ||
| IWCNM | Homogeneity | 13.856 | 0.001 | -8.25 | 22 | 0.000 |
| Heterogeneity | -6.494 | 8.567 | 0.000 | |||
| RCCM | Homogeneity | 1.251 | 0.275 | 1.914 | 22 | 0.069 |
| Heterogeneity | 1.765 | 13.111 | 0.101 | |||
Figure 3 APS degree of the YRD and PRD based on the IWCNM (a) and RCCM (b) |
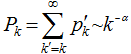
Figure 4 Distribution degree of the YRD (a) and PRD (b) based on the IWCNM and RCCM |
Table 5 Regression equations of rank-size degree |
| Algorithm | Regression equation | Coefficient of determination (R²) | |
|---|---|---|---|
| YRD | IWCNM | Ln(Pk) = -0.613ln(k)+0.088 | 0.966 |
| RCCM | Ln(Pk) = -0.751ln(k)+0.043 | 0.966 | |
| PRD | IWCNM | Ln(Pk) = -0.792ln(k)+0.026 | 0.925 |
| RCCM | Ln(Pk) = -1.176ln(k)+0.271 | 0.956 |
Figure 5 Comparison of APS city networks based on the IWCNM and RCCM |
Table 6 Comparison of the central degree nodality of the IWCNM and RCCM |
| City | Nodality | In-degree | Out-degree | Closeness | Betweenness | |
|---|---|---|---|---|---|---|
| IWCNM | RCCM | |||||
| Shanghai | 1.000 | 1.000 | 0.672 | 1.000 | 1.000 | 1.000 |
| Nanjing | 0.659 | 0.500 | 0.689 | 0.423 | 0.349 | 0.270 |
| Zhenjiang | 0.265 | 0.156 | 0.820 | 0.000 | 0.017 | 0.000 |
| Suzhou | 0.467 | 0.325 | 0.705 | 0.219 | 0.122 | 0.068 |
| Nantong | 0.284 | 0.169 | 0.885 | 0.000 | 0.032 | 0.005 |
| Yangzhou | 0.236 | 0.163 | 0.852 | 0.000 | 0.023 | 0.000 |
| Changzhou | 0.276 | 0.191 | 0.836 | 0.036 | 0.061 | 0.016 |
| Wuxi | 0.392 | 0.291 | 1.000 | 0.115 | 0.213 | 0.080 |
| Taizhou (Jiangsu) | 0.246 | 0.156 | 0.820 | 0.000 | 0.012 | 0.000 |
| Hangzhou | 0.697 | 0.475 | 0.836 | 0.362 | 0.340 | 0.176 |
| Huzhou | 0.203 | 0.138 | 0.721 | 0.000 | 0.012 | 0.000 |
| Jiangxing | 0.246 | 0.156 | 0.820 | 0.000 | 0.019 | 0.000 |
| Ningbo | 0.476 | 0.328 | 0.508 | 0.265 | 0.140 | 0.080 |
| Shaoxing | 0.231 | 0.144 | 0.754 | 0.000 | 0.051 | 0.000 |
| Taizhou (Zhejiang) | 0.250 | 0.141 | 0.738 | 0.000 | 0.011 | 0.000 |
| Zhoushan | 0.005 | 0.006 | 0.033 | 0.000 | 0.005 | 0.000 |
| Guangzhou | 0.813 | 0.472 | 0.770 | 0.373 | 0.443 | 0.257 |
| Shenzhen | 0.868 | 0.756 | 0.656 | 0.724 | 0.624 | 0.644 |
| Dongguan | 0.323 | 0.163 | 0.557 | 0.065 | 0.047 | 0.048 |
| Zhuhai | 0.264 | 0.103 | 0.541 | 0.000 | 0.042 | 0.000 |
| Foshan | 0.309 | 0.119 | 0.623 | 0.000 | 0.036 | 0.000 |
| Zhaoqing | 0.178 | 0.063 | 0.328 | 0.000 | 0.004 | 0.000 |
| Zhongshan | 0.245 | 0.097 | 0.508 | 0.000 | 0.021 | 0.000 |
| Jiangmen | 0.185 | 0.072 | 0.377 | 0.000 | 0.010 | 0.000 |
| Huizhou | 0.207 | 0.081 | 0.377 | 0.011 | 0.020 | 0.019 |
Table 7 Classification of the cities based on the RCCM |
| Characteristics | City | |
|---|---|---|
| A | Significantly high nodality, closeness, and betweenness | Shanghai, Shenzhen, Guangzhou, Nanjing, and Hangzhou |
| B | Significantly high nodality and closeness | Suzhou, Nantong, Changzhou, Wuxi, Ningbo, Shaoxing, and Dongguan |
| C | Significantly low nodality | Zhuhai and Foshan |
| D | Significantly low closeness | Zhenjiang, Yangzhou, Huzhou, Jiangxing, Taizhou (Jiangsu), and Taizhou (Zhejiang) |
| E | Significantly low nodality and closeness | Zhaoqing, Zhongshan, Jiangmen, Huizhou, and Zhoushan |
Figure 6 Model map based on the RCCM for three regions |
The authors have declared that no competing interests exist.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
/
| 〈 |
|
〉 |