

Journal of Geographical Sciences >
Evaluating the suitability of TRMM satellite rainfall data for hydrological simulation using a distributed hydrological model in the Weihe River catchment in China
*Corresponding author: Yang Shengtian (1965-), Professor, E-mail:yangshengtian@bnu.edu.cn
Author: Zhao Haigen (1983-), PhD Candidate, specialized in hydrological simulation and remote sensing. E-mail:zhaohaigen1983@163.com
Received date: 2014-01-21
Accepted date: 2014-06-12
Online published: 2015-02-15
Supported by
National Key Technology P&D Program, No.2012BAB02B00
The Fundamental Research Funds for the Central Universities
Copyright
The objective of this study is to quantitatively evaluate Tropical Rainfall Measuring Mission (TRMM) data with rain gauge data and further to use this TRMM data to drive a Distributed Time-Variant Gain Model (DTVGM) to perform hydrological simulations in the semi-humid Weihe River catchment in China. Before the simulations, a comparison with a 10-year (2001-2010) daily rain gauge data set reveals that, at daily time step, TRMM rainfall data are better at capturing rain occurrence and mean values than rainfall extremes. On a monthly time scale, good linear relationships between TRMM and rain gauge rainfall data are found, with determination coefficients R2 varying between 0.78 and 0.89 for the individual stations. Subsequent simulation results of seven years (2001-2007) of data on daily hydrological processes confirm that the DTVGM when calibrated by rain gauge data performs better than when calibrated by TRMM data, but the performance of the simulation driven by TRMM data is better than that driven by gauge data on a monthly time scale. The results thus suggest that TRMM rainfall data are more suitable for monthly streamflow simulation in the study area, and that, when the effects of recalibration and the results for water balance components are also taken into account, the TRMM 3B42-V7 product has the potential to perform well in similar basins.
ZHAO Haigen , YANG Shengtian , WANG Zhiwei , ZHOU Xu , LUO Ya , WU Linna . Evaluating the suitability of TRMM satellite rainfall data for hydrological simulation using a distributed hydrological model in the Weihe River catchment in China[J]. Journal of Geographical Sciences, 2015 , 25(2) : 177 -195 . DOI: 10.1007/s11442-015-1161-3
Figure 1 Location of the Weihe River catchment in the Yellow River Basin and the distribution of stations |
Figure 2 Map of land use in the study area |
Figure 3 Soil types in the study area |
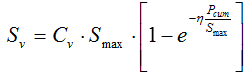
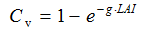
Figure 4 Framework of the DTVGM (a) and vertical profile of hydrological processes (b) in a grid cell |
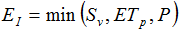 (3)
(3) (4)
(4)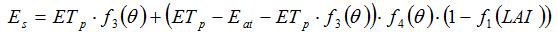
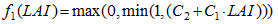
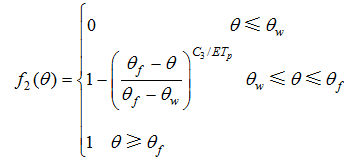
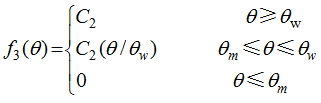
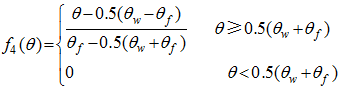
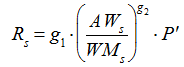
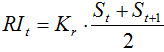
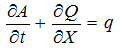
Table 1 Parameters optimized in the DTVGM hydrological simulation |
| Name | Min | Max | Description | Initial value |
|---|---|---|---|---|
| g1 | 0.20 | 0.50 | Coefficient of time-variant gain factor | 0.25 |
| Ra | 0.10 | 0.60 | Initial ratio of soil water in the soil layer | 0.20 |
| Kr | 0.0001 | 0.001 | Storage-outflow coefficient for the soil layer | 0.00015 |
| C1 | 0.001 | 1.00 | Dimensionless fitting parameter for ET | 0.40 |
| C2 | 0.60 | 0.80 | Dimensionless fitting parameter for ET | 0.60 |
| C3 | 5.00 | 20.00 | Dimensionless fitting parameter for ET | 15.00 |
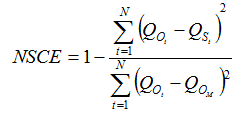
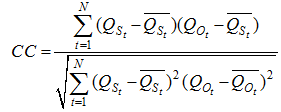
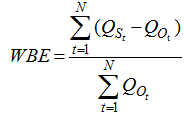
Table 2 Comparison of statistical indices between averaged TRMM rainfall and rain gauge rainfall |
| Year | Areal average (mm/d) | Standard deviation (mm) | Maximum daily rainfall (mm/d) | Maximum 5-day rainfall (mm/5d) | Annual rainfall (mm/y) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Gauge | TRMM | Gauge | TRMM | Gauge | TRMM | Gauge | TRMM | Gauge | TRMM | |
| 2001 | 1.29 | 1.35 | 2.99 | 2.91 | 23.01 | 21.77 | 94.15 | 87.76 | 468.91 | 496.30 |
| 2002 | 1.26 | 1.24 | 3.36 | 2.90 | 36.12 | 23.91 | 105.36 | 94.05 | 458.57 | 456.12 |
| 2003 | 2.15 | 2.14 | 4.87 | 4.34 | 36.82 | 31.14 | 142.07 | 118.28 | 782.92 | 781.17 |
| 2004 | 1.31 | 1.35 | 3.19 | 2.94 | 23.92 | 27.73 | 90.46 | 86.92 | 480.03 | 493.15 |
| 2005 | 1.56 | 1.73 | 3.84 | 3.94 | 27.04 | 32.03 | 120.48 | 121.09 | 570.38 | 631.24 |
| 2006 | 1.52 | 1.36 | 3.32 | 2.68 | 21.62 | 18.82 | 94.00 | 77.42 | 555.04 | 497.86 |
| 2007 | 1.58 | 1.52 | 3.54 | 3.65 | 25.73 | 35.32 | 99.00 | 121.90 | 575.02 | 556.21 |
| 2008 | 1.26 | 1.44 | 3.09 | 3.42 | 22.67 | 25.64 | 88.16 | 109.00 | 462.70 | 525.65 |
| 2009 | 1.40 | 1.47 | 3.07 | 3.25 | 23.26 | 24.62 | 85.92 | 99.89 | 512.63 | 525.22 |
| 2010 | 1.61 | 1.55 | 4.27 | 3.42 | 44.29 | 22.65 | 133.07 | 95.49 | 589.15 | 565.08 |
Figure 5 Distribution of daily rainfall in different rainfall categories and relative contribution to total rainfall, 2001-2010 |
Figure 6 Scatter plots of monthly rainfall from TRMM and rain gauge data for the seven national meteorological stations and the areal average data |
Table 3 Comparison of daily observed and simulated streamflow under two calibration scenarios |
| Precipitation products | Scenario I | Scenario II | |||||
|---|---|---|---|---|---|---|---|
| NSCE | WBE (%) | CC | NSCE | WBE (%) | CC | ||
| Calibration period | |||||||
| Gauge | 0.69 | 18.71 | 0.84 | 0.68 | 14.37 | 0.83 | |
| TRMM | 0.59 | 21.96 | 0.78 | 0.60 | 18.02 | 0.78 | |
| Validation period | |||||||
| Gauge | 0.55 | -18.85 | 0.78 | 0.52 | -23.85 | 0.74 | |
| TRMM | 0.48 | -15.38 | 0.71 | 0.50 | -19.91 | 0.72 | |
Figure 7 Comparison of observed and simulated hydrographs using daily rain gauge data at Xianyang hydrological station |
Figure 8 Comparison of observed and simulated hydrographs using daily TRMM data at Xianyang hydrological station |
Table 4 Comparison of monthly observed and simulated streamflow under two calibration scenarios |
| Precipitation products | Scenario I | Scenario II | |||||
|---|---|---|---|---|---|---|---|
| NSCE | WBE (%) | CC | NSCE | WBE (%) | CC | ||
| Gauge | 0.64 | -0.84 | 0.83 | 0.64 | -5.58 | 0.82 | |
| TRMM | 0.67 | 2.52 | 0.84 | 0.68 | -1.78 | 0.84 | |
Figure 9 Comparison of observed and simulated discharge with monthly TRMM and rain gauge data at Xianyang hydrological station |
Table 5 DTVGM model parameter values calibrated with different rainfall inputs for the calibration period |
| Parameters | Gauge | TRMM |
|---|---|---|
| g1 | 0.23 | 0.22 |
| Kr | 0.0006 | 0.0002 |
| C1 | 0.50 | 0.52 |
| C2 | 0.78 | 0.66 |
| C3 | 10.00 | 9.96 |
| Ra | 0.15 | 0.51 |
Figure 10 Relative changes to water balance components in models based on rain gauge and TRMM rainfall data |
The authors have declared that no competing interests exist.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
/
| 〈 |
|
〉 |