EN中文

Journal of Geographical Sciences >

2015 , Vol. 25 >Issue 1: 69 - 84

DOI: https://doi.org/10.1007/s11442-015-1154-2

Orginal Article

Assessment of meteorological disasters based on information diffusion theory in Xinjiang, Northwest China

  • WU Meihua , 1 ,
  • CHEN Yaning , 2, * ,
  • XU Changchun 1
Expand
  • 1. Key Laboratory of Oasis Ecology, School of Resource and Environmental Sciences, Xinjiang University, Urumqi 830046, China
  • 2. State Key Laboratory of Desert and Oasis Ecology, Xinjiang Institute of Ecology and Geography, CAS, Urumqi 830011, China

*Corresponding author: Chen Yaning (1958-), Professor, E-mail:

Author: Wu Meihua, PhD, specialized in risk assessment of natural disasters. E-mail:

Received date: 2014-01-07

  Accepted date: 2014-05-05

  Online published: 2015-01-15

Supported by

National Natural Science Foundation of China, No.41305125

No.U1203281

National Basic Research Program of China (973 Program), No.2010CB951003

Copyright

Journal of Geographical Sciences, All Rights Reserved
Fold

Abstract

Data of flood, drought, hailstorms, and low temperature events in Xinjiang from 1949 to 2012 were analyzed with the diffusion method to assess the risk of the most common types of disasters in Xinjiang. It was proved that the frequency and intensity of meteorological disasters of the study area showed an increasing trend associated with global warming. Among the four types of disasters, surpass probability of drought was the largest, followed by hailstorm, low temperature and flood in turn. Moreover, the wavelet method analysis revealed that greater oscillations had occurred since 2000, which may be associated with the occurrence of extreme climatic changes. The spatial distribution of frequencies reveals that the northern slope of Tianshan Mountains is a multiple disaster area, the southern slope of Tianshan is the area where more floods and hailstorms occur, and the west of Turpan-Hami Basin is the area wind is prevalent. The relationships between disaster-affected areas and corresponding meteorological and socio-economic indexes were also analyzed. It indicated that there were significant positive correlations between the areas affected and the most meteorological and socio-economic indicators except the grain acreage.

Key words： risk assessment; meteorological disaster; information diffusion; Xinjiang

Cite this article

WU Meihua , CHEN Yaning , XU Changchun . Assessment of meteorological disasters based on information diffusion theory in Xinjiang, Northwest China[J]. Journal of Geographical Sciences, 2015 , 25(1) : 69 -84 . DOI: 10.1007/s11442-015-1154-2

1 Introduction

Global climate change is causing rising temperature and non-uniform rainfall in many parts of the world. According to the IPCC’s Fourth Assessment Report (IPCC, 2007), the intensity and frequency of natural disasters have greatly changed over the past 60 years, and areas affected by drought have expanded while heavy rain events have increased. Likewise, wind such as tropical cyclones and hurricanes (Peter et al., 2005; Kerry 2005; James et al., 2008; Mansuer and Lutubula, 2012), floods (Juraj, 2009; Paul et al., 2002; Wang et al., 2008), and low temperature (Yang et al., 2012; Yang et al., 2008) have also become more intense and their time duration has significantly extended. If these trends continue, the frequency and intensity of extreme weather events are expected to increase in the future. Computer simulations show that the frequency of heat waves and heavy precipitation will likely continue to rise, and the frequency and time duration of drought and flood will increase (IPCC, 2007).
Historically, Xinjiang in Northwest China had a dry climate. With the change of history and the interference of human activities, however, the climate here is changing. During the past 50 years, especially recent 30 years, the region has experienced an intense changing trend from warm-dry to warm-wet conditions (Hu et al., 2001; Hu et al., 2002; Wu et al., 2001). Researches indicate that temperature and precipitation have increased significantly in this region, with northern Xinjiang experiencing greater increases than southern Xinjiang (Li, 2013; Yang, 1998). At the same time, the frequency and intensity of meteorological disasters such as wind, hailstorm, extreme temperature and drought have also risen, negatively impacting agriculture-stock production and transportation (Cao et al., 2009, Mansur, 2012, Sun, 2011; Zhang and Zhang, 2011). Oasis irrigation farming, the main form of agriculture in Xinjiang, is the industry mostly affected by natural disasters. Under climate change, the increasing frequency and intensity of extreme weather events will have serious consequences on the oasis economy and agricultural production. At the same time, the increasing population and rapidly developing economy will make the fragility of the ecological environment more evident. Environmental suitability, ecological stability and recovery ability are crucial for arid agricultural production, and thus it is essential to estimate the risk of the main meteorological disasters.
Traditionally, the essence of natural disaster risk is the probability distribution of uncertainties in magnitude and time of a disaster. The risk assessment is to find out a scientific way to estimate the probability distribution. Probability statistics offer the theoretical basis for risk assessment (Huang, 1998). If the historical data of disaster-inducing factors or samples are complete in both temporal and spatial, and also the number of samples is more than 30, the probability can be calculated by using frequency statistics or probability distribution function. Otherwise, fuzzy information method is proposed to centralize and obfuscate samples, offsetting the information deficient problem (Parzen, 1962). The method can change a single-valued sample into a set-valued one. The simplest model is the Gaussian diffusion model (Huang, 1998). It was applied in this paper to analyze the risk of meteorological disasters, droughts, floods, hailstorms and low temperatures, in Xinjiang. There have been some studies concerned with natural disasters in Xinjiang (Sun, 2011; Yang and He, 2005; Wang, 2008). They paid more attention to the temporo-spatial distribution of disasters based on historical data, and seldom concerned with risk assessment of disasters. The methods they used were logarithmic function method and gray relational model. The risk assessment of information diffusion based on fuzzy theory can deal with small samples and accurately calculate the risk of disasters. It is vital to assess the risk of meteorological disasters to forecast and reduce the loss.

2 Material and methods

2.1 Study area

Xinjiang is located in central Eurasia, in the arid western part of Northwest China. The area is characterized by a typical continental climate featuring low precipitation. Three mountain ranges (the Altai Mountains, the Tianshan Mountains, and the Kunlun Mountains) span the region and two major basins (the Junggar Basin in northern Xinjiang and the Tarim Basin in southern Xinjiang) are situated between them (Jiang, 2005b). Xinjiang is divided into southern and northern areas by its natural landscape. The Turpan-Hami Basin, formed from the Tianshan’s fault-line valley, demarcates southern, northern, and eastern Xinjiang (Figure 1). In this paper, seven geographic units are divided, i.e., southern slope of Altai Mountains, northern slope of Tianshan Mountains, Pamirs, northern slope of Kunlun Mountains and eastern part of Tianshan Mountains.
Figure 1 Map of the study area
On the whole, differences in altitude and vertical gradient cause more variations in regional climate than latitude differences. Under the westerly-prevailing weather system and polar Arctic ocean system, warm and cold weather frequently alternate in spring, causing strong winds, sandstorms and cold wave disasters. In summer, high amounts of precipitation in the mountains cause flooding and secondary disasters, while hailstorms often occur in mid-to-low mountain areas and the piedmont belt. In both spring and summer, temperatures rise rapidly and there is scarce precipitation, often leading to agricultural drought. In winter, the polar winds sweep across northern Xinjiang, causing snowstorms and extreme plunging temperatures (Wen and Shi, 2006).
Meteorological disasters in Xinjiang share the following characteristics: wide-ranging effects, high frequency, sudden onset, and a higher likelihood of causing a chain of events. Assessment risk of the main meteorological disasters can provide a scientific basis for disaster prevention and mitigation.

2.2 Data sources

The meteorological disaster data were obtained from Chinese Planting Information, A history of calamities in Xinjiang and Meteorological disaster ceremony of China-Xinjiang volume. Disaster indexes of cover areas were affected by flood, drought, hailstorms, and extreme low temperature events in Xinjiang from 1949 to 2012. The statistical data from 1949 to 2012 were cited by Xinjiang Uygur Autonomous Region Statistical Yearbook. Meteorological data were obtained from the Xinjiang Meteorological Bureau, the Desert and Oasis Meteorological Institute in Xinjiang, and various hydrological stations in Xinjiang. Annual precipitation and temperature data from 1961 to 2010 were obtained from meteorological stations.

3 Methods

In this paper, information diffusion theory was used to assess meteorological disaster risk. Furthermore, by applying the Morlet wavelet method to analyze the disaster oscillation period, the correlation coefficients between the affected areas and economic indexes were calculated.

3.1 Evaluation indexes

Numerous risk indexes can be used to assess meteorological disaster risk. In this paper, we chose affected ratio, covered ratio, and intensity of disaster for floods, droughts, hailstorms, and extreme low temperatures. Affected area, covered area and demolished area are often used in disaster information statistics by agricultural sector. In general, area reduced more than 10% due to disaster is included in affected area; area reduced more than 30% due to disaster is included in covered area; area reduced more than 80% due to disaster is included in demolished area (Zhang et al., 2009) and disaster intensity refers to the ratio between the covered area and the affected area. A higher value indicates a more severe disaster, and vice versa. Equations expressing these ratios are as follows:
where Xa is affected ratio by disaster (%); Xc is covered ratio by disaster, %; X is intensity of disaster (%); Sa is affected area by disaster (1×103 hm2); Sc is covered area by disaster (1×103 hm2); S is sown area of farm crops (1×103 hm2).

3.2 Risk assessment methods of disasters

Information diffusion refers to transforming a traditional data sample point into a fuzzy set. The principle undergirding information diffusion is affirmation: when a knowledge sample is given, it can be used to compute a relationship. The result deduced directly from this sample is called “non-diffusion estimation”. When this sample is incomplete, there must be an appropriate diffusion function and a corresponding arithmetic formula, which makes the diffusion estimation closer to the real relationship than the non-diffusion estimation. As the purpose of information diffusion is to search for useful information and enhance the identification precision of the system, technology of this kind is thus called Fuzzy Information Optimization Processing Technology (Huang, 2002b).
Information diffusion is a processing method of abstract mathematics that can deal with the sample using a set numerical method (Huang 2000, 2002a). A single-valued sample can be transformed into a set numerical-valued sample through this technology. The simplest model is the normal diffusion model. If the index field of meteorological disaster can be represented as U={u1, u2, ..., um}, then the information carried by a single-valued observation sample of xi can be diffused into each point in the field U according to the following equation:
where h is the diffusion coefficient, which can be determined according to the maximum and minimum values of the samples and the sample number in the set (Chatman, 1986; Huang, 1997, 2001). If we let:
then the related attaching function of the fuzzy subset can be represented as follows:
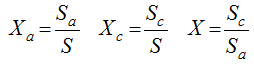
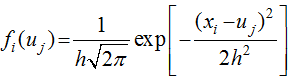
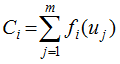
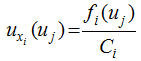
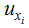The function of can be called the normalized information distribution of sample xi.
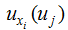A good result for risk analysis can be obtained through the treatment of the function of
. If we let x1, x2,..., xn be the n specified observation values, then the function can be called the information quantum diffused from the sample of X={x1, x2, ..., xn} to the observation point of μj. This can be represented as: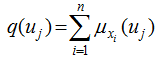
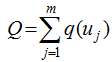
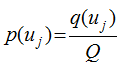
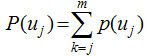
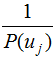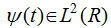The physical meaning of the above function is that if the observation value of water shortage can only be chosen as one of the values in the series of u1, u2, ... um, then the sample number with the observation value of uj can be determined as q(uj) through the information diffusion from the observation set of x1, x2,..., xn, in regards to all values of xi as the representatives of the samples. It is obvious that the value of q(uj) is generally not a positive integer, but it is certain to be a number no less than zero. Furthermore, let:
where Q should be the summation of the sample number on each point of uj. The function should thus be the frequency value of the sample appearing on the point of uj, and the value can be taken as the estimated value of the probability. This can be represented as:
The probability value transcending of uj should then be as follows:
and the value of p(u≥uj) should be the required value for the risk assessment. The surpass probability as P(uj) of function 8, the recurrence interval / return period as .

3.3 Wavelet analysis

In this paper, by using the Morlet wavelet analysis to research a time series of disasters, the function of multi-resolution time-frequency can clearly reveal the various periods hidden in the time series. As well, it can fully reflect the changing trend of the system in different time scales and show changing trends of various time-frequencies for qualitative estimates of future development trends (Liu, 2009).
The basic idea of wavelet analysis is to use a set of wavelet function systems close to a signal or function. The wavelet function is thus the key to wavelet analysis because it is a kind of function that quickly attenuates to zero (the wavelet function) , thereby satisfying: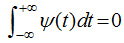
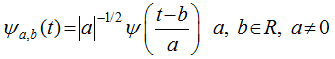
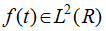so that ψ(t) is regarded as a mother wavelet. By using scale expansion and horizontal shifts on the time axis, a set of function systems can be constituted:
where ψa,b(t) is a baby wavelet; a is a scale factor used to express period length; and b is a shift factor used to express time shift. It is essential to choose the appropriate mother wavelet function as the premise to perform the wavelet analysis.
If ψa,b(t) is the baby wavelet given by (10) and is regarded as a given energy limited signal, the Continuous Wavelet Transform (CWT) is: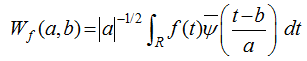
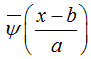where Wf (a, b) is a wavelet transform coefficient and f(t) is a signal of quadratically inte-
grable function. Where a is a scale factor, b is a shift factor, and is complex conjugate function of 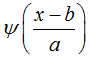. Because most of the time series data observed in geography are a discrete set function f(kΔt), (k=1, 2, …, N; Δtas sample interval), then (11) discrete wavelet transform is as follows: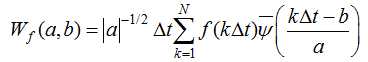
Functions (11) or (12) show the basic principle of wavelet analysis by increasing or decreasing scale a to achieve low frequency or high frequency information of signal, then analysis overview or detail of signal, to complete different spatial-temporal scales of signal analysis.
In practical research, the priority is first to obtain wavelet coefficients through wavelet transformation equations and then the wavelet coefficient analysis time-frequency variation characteristics of a time series.

4 Results and discussion

4.1 Disaster characteristics and changing trends

From Table 1, we can see that four kinds of disaster losses show increasing trends in Xinjiang, with affected areas and covered areas showing a sharp increase since the 1980s. More specifically, in the 1980s, 1990s and 2000s, flood-related covered areas increased 5.45 times, 9.18 times and 7.85 times, respectively, compared with the 1950s. Similarly, drought-related covered areas increased 5 times, 4.19 times and 9.42 times, respectively, compared with the 1950s. Compared with the 1960s, hailstorms-related covered areas increased 2.98 times, 6.08 times, and 9.89 times in the 1980s, 1990s, and 2000s, respectively. Furthermore, in the decadal time scale for covered areas, flooding shows three periods of strong disasters in the 1980s, 1990s, and 2000s; drought shows strong disasters in the 1960s, 1980s, and 2000s; hailstorms shows strong disasters in the 1970s, 1990s, and 2000s; and low temperature events were the worst in the 1970s, 1990s, and 2000s. The highest losses of the four kinds of disasters occurred in the 2000s, while the highest losses and growth rates are in descending order: drought, hailstorms, low temperature events, and floods.
Table 1 Affected area and covered area by decadal meteorological disasters
Age M. A.
A1 A2 B1 B2 C1 C2 D1 D2
1950s 12.3 5.22 70.47 33.21 6.89
1960s 13.99 4.83 205.41 143.95 25.07 12.27
1970s 11.65 4.28 200.41 118.52 55.64 45.33 57.44 56.83
1980s 95.02 28.45 243.73 166.03 74 36.67 36.87 17.33
1990s 80.02 47.91 332.82 139.26 132.4 74.67 113.57 54.8
2000s 73.8 39.57 455.79 312.78 228.05 121.33 176.89 102.91

*M.A. is mean area, A1 is affected area by flood, 1×103 hm2, A2 is covered area by flood, 1×103 hm2, B1 is affected area by drought, 1×103 hm2, B2 is covered area by drought, 1×103 hm2, C1 is affected area by hailstorms, 1×103 hm2, C2 is covered area by hailstorms, 1×103 hm2, D1 is affected area by low temperature, 1×103 hm2, D2 is covered area by low temperature, 1×103 hm2.

**The data of Table 1 are obtained from Chinese Planting Information.

In Figure 2, we see that flood, drought, hailstorms and low temperature events show increasing trends, with the growth rate of affected ratios for flood, drought, hailstorms and low temperature events being 17.49%/10a, 60.28%/10a, 55.6%/10a, and 64.43%/10a, respectively. The slope of affected ratios from drought is the steepest among the four disasters, indicating that drought is the main disaster in this region (Figure 2b). Detailed analyses show that, since the 1980s, flood-related covered ratios and affected ratios are steadily increasing, with covered ratios reaching a peak in 2002 from a minimum in the 1960s (Figure 2a). From Figure 2b, we can see that, since the 1980s, drought presents a growing trend, reaching a covered ratio peak in 2008 following a minimum in the 1950s. Similarly, hailstorms-related covered ratios and affected ratios significantly increased since the 1970s (Figure 2c), suddenly fell in 2005, and then reached a maximum in 2009 (from a 1960s minimum). Covered ratios and affected ratios for low temperature events have also continued to grow since 1995, reaching a maximum in 2008 (Figure 2d). Because disaster-related losses have substantially increased, covered ratios reached a maximum in the 2000s.
Figure 2 Affected and covered area by disasters in Xinjiang (a. Flood; b. Drought; c. Hailstorms; d. Low temperature)

4.2 Spatial distribution of disasters and the potential reasons

Frequencies of four disasters, drought, flood, hailstorms and wind, are mapped to show the spatial distribution of disasters in Xinjiang over the last 50 years (Figures 3a-d). More droughts are found to occur in the mid northern slope of Tianshan Mountains, followed by the southern slope of Altai Mountains, Turpan-Hami Basin, and the mid northern slope of Kunlun Mountains (Figure 3a). Fewer droughts are found at the west edge of Tarim Basin, southern slope of Tianshan and Ili Valley. Overall, drought is more likely to appear in northern Xinjiang than southern Xinjiang, which is seemed to be contrary to the fact that climate in northern Xinjiang is wetter than that of southern Xinjiang. Drought in this paper refers to agricultural drought. In southern Xinjiang, several major rivers, such as the Aksu, Yarkant, Hotan, Weigan and Tarim rivers, feed the agriculture with relatively abundant water, so agricultural drought is relatively less. In northern Xinjiang, however, stock breeding is more developed than farming. Large areas of natural grassland exist on the southern slope of Altai Mountains and northern slope of Tianshan. Natural grasslands are sensitive to drought. Under global warming and without the constant water supply, it is easier to cause the consecutive drought from spring to summer and the subsequent agricultural drought.
Floods in Xinjiang mainly originated from mountain area and induced by ice-snow melt and precipitation. As shown in Figure 3b, floods occurred mainly on both slopes of Tianshan Mountains, and seldom in Altai Mountains (Ma, 1994; Ma and Xi, 1997). Due to the increase of heavy rain in summer, floods have occurred more frequently since the late 1980s.
Intersections of the Turpan-Hami Basin and eastern Tianshan, and the middle part of northern Tianshan, are the areas where wind is prevalent (Figure 3c). Less wind disasters occur in Ili Valley and southern slope of Altai Mountains. Obviously, eastern Xinjiang was prone to be affected by wind disaster. It can be attributed to the unique geographic environment that makes the wind distributed complicated. Each cold air invasion from Siberia firstly arrives at Xinjiang from the wind gaps and valleys distributed in the northwest. The Tianshan standing at the southern edge of Junggar Basin then obstructs the wind and makes it blow eastward along the northern slope and finally reaches the Turpan-Hami Basin, the lowest depression in China. Owing to the lifting effect of mountains, it is easier to cause strong storms while wind goes from west to east. It not only affects the agriculture and animal husbandry but also the traffic severely.
Figure 3 The spatial distribution of frequencies of disasters in Xinjiang from 1949 to 2000

(a. Drought; b. Flood; c.Wind; d. Hailstorms)

Hailstorm’s spatial distribution is similar to that of floods, mainly over the southern slope and the middle-west of northern slope of Tianshan (Figure 3d). The distribution is closely related to rain cloud and rainstorm paths. High standing Tianshan, horn-like valley with mouth opening eastward, along with the leeward slope, all benefit for the development of cumulus changing to hailstorm cloud. If encounters favorable weather conditions, hailstorm forms. Hailstorms in Xinjiang are characterized by the following distribution pattern: more in mountain valleys, leeward slopes, and horn-like river valleys; less in the center of basins (Wen and Shi, 2006).
Comprehensively view, the northern slope of Tianshan is the area where four types of disasters, especially the flood and drought, are prevalent. The southern slope of Tianshan is the area where more floods and hailstorms occur. The Turpan-Hami Basin in eastern Xinjiang is the area where floods, droughts and wind are prone to occur.

4.3 Disaster risk assessment

The recurrence interval and surpass probability of disaster risk can be obtained by equations. (1)-(8). Table 2 shows that when the frequency of ratios affected by the four types of disasters is the highest, the return period of disasters is the shortest. The recurrence interval and surpass probability of disaster risk sequence shows that drought is the strongest, followed by hailstorms, low temperature, and flood. The surpass probability of drought is the strongest, and the recurrence interval is the shortest.
Table 2 Surpass probability of ratio affected by all kinds of disasters
Ratio affected 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13
1 S.P. 0.75 0.52 0.37 0.24 0.16 0.14 0.11 0.08 0.05 0.04 0.04 0.03 0.01
R.I. 1.34 1.93 2.70 4.14 6.12 7.09 8.84 13.30 19.5 26.80 28.10 32.60 86.80
2 S.P. 1 0.98 0.96 0.93 0.89 0.83 0.76 0.70 0.63 0.54 0.44 0.33 0.25
R.I. 1 1.02 1.04 1.08 1.13 1.21 1.31 1.43 1.60 1.85 2.28 3.01 4.00
3 S.P. 0.97 0.85 0.69 0.55 0.40 0.28 0.22 0.18 0.12 0.09 0.07 0.05 0.03
R.I. 1.03 1.18 1.45 1.81 2.49 3.60 4.53 5.71 8.23 10.6 13.70 19.20 38.20
4 S.P. 0.8 0.58 0.39 0.26 0.20 0.18 0.16 0.14 0.12 0.09 0.08 0.07 0.06
R.I. 1.25 1.72 2.55 3.78 4.99 5.67 6.2 6.97 8.25 10.6 13.00 14.80 17.90
Ratio affected 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
2 S.P. 0.2 0.16 0.13 0.11 0.09 0.08 0.07 0.07 0.07 0.06 0.04 0.02
R.I. 5.09 6.31 7.83 9.51 11.30 12.9 13.80 14.1 14.60 16.80 23.70 45.30
4 S.P. 0.04 0.04 0.04 0.04 0.03 0.02 0.01
R.I. 23.3 27.3 28.2 28.4 30.2 40.20 89.30

**1 is Flood, 2 is Drought, 3 is Hailstorms, 4 is Low temperature;

*S.P. is Surpass probability of disaster risk, %; R.I. is Recurrence interval, year.

Although regional annual precipitation and runoff are increasing, the distribution of precipitation and runoff during the year is non-uniform. Since the mid-1980s, regional drought has increased, which is different from the increasing trend of precipitation and runoff during the same timeframe (Jiang, 2005a). Hailstorms is hailstorm accompanied by strong wind; its frequency is only slightly lower than drought and, like drought, causes major damage to crops. These storms are strongly localized, often occurring in basins and valleys, on the leeward side of mountains, and in river valleys. Exceptionally strong hailstorms occurred in 2011 and 2012. Another crop-affecting disaster is low temperature events that occur during cropping season, causing crop losses in the cotton, forestry and fruit industries. Xinjiang traditionally has a dry climate, but the recent trend towards uneven distribution of precipitation during the year accompanied by strong floods has led not only to crop losses but also destruction of facilities.
From Table 3, the surpass probability of ratio covered by disasters shows that the maximum value is 14%. When the range is from 1% to 10%, the surpass probability of drought is the highest among all the disasters, the return period is the shortest, followed by hailstorms, low temperature events, and floods. This shows that the surpass probability of ratios for covered area by drought is the most and that the surpass probability of ratios for covered area by flood is the least.
According to integrated disaster risk analysis (Table 4), when ratios affected by integrated disasters are from 10% to 20%, the surpass probability is the highest and the recurrence interval is the shortest, (about 1-2 years). When ratios covered by integrated disaster are around 10%, the surpass probability is the highest, and the recurrence interval is about 2 years. Furthermore, when the intensity of integrated disaster is from 10% to 50%, the surpass probability is the highest and the return period is about 1-2 years.
Table 3 Surpass probability of ratio covered by all kinds of disasters
Ratio covered 0.01 0.02 0.03 0.04 0.05 0.06 0.07
Flood S.P. 0.5 0.19 0.11 0.06 0.003
R.I. 1.99 5.4 9.48 15.4 292
Drought S.P. 0.98 0.94 0.9 0.8 0.61 0.47 0.35
R.I. 1.02 1.07 1.11 1.25 1.64 2.14 2.82
Hailstorms S.P. 0.77 0.58 0.39 0.21 0.12 0.04 0.03
R.I. 1.29 1.73 2.55 4.76 8.5 23.4 28.7
Low
temperature		 S.P. 0.56 0.29 0.16 0.12 0.1 0.08 0.06
R.I. 1.79 3.47 6.28 8.68 9.87 12.3 16.7
Ratio covered 0.08 0.09 0.1 0.11 0.12 0.13 0.14
Drought S.P. 0.23 0.16 0.1 0.05 0.03 0.004
R.I. 4.33 6.26 9.71 20.2 34.2 249
Wind
hailstorms		 S.P. 0.01
R.I. 93.3
Low
temperature		 S.P. 0.04 0.04 0.04 0.04 0.04 0.03 0.01
R.I. 24.4 27.8 28 28 28.6 38.1 135

**R.P. is Surpass probability of disaster risk, %; R.I. is Recurrence interval, year

Table 4 Surpass probability of integrated disaster risk
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
A.I. S.P. 0.99 0.62 0.09 0.04 0.01
R.I. 1.01 1.61 11.5 28 164
C.I. S.P. 0.63 0.04 0.01
R.I. 1.6 27.5 129
I.I. S.P. 1 1 1 0.89 0.67 0.35 0.08 0.02
R.I. 1 1 1 1.13 1.5 2.85 12.7 60.5

**A.I. is Ratio affected by integrated disaster, C.I. is Ratio covered by integrated disaster, I.I. is Intensity of integrated disaster; *S.P. is Surpass probability of disaster risk, %; R.I. is Recurrence interval, year.

The surpass probability of ratios covered by disaster shows that drought was the largest, followed by hailstorms, low temperature, and flood in turn. When ratios covered by disasters are from 1% to 9%, the surpass probability of all kinds of disasters is high and the recurrence interval is short. The order of surpass probability of ratios affected by disasters is the same as ratios covered by disasters; the higher ratios are affected and covered by disasters, the lower the surpass probability of disasters and the longer recurrence interval. When ratios affected by integrated disasters range from 10% to 20%, the surpass probability is the highest and the recurrence interval of disaster is about 1-2 years.

4.4 Periods of disaster occurrence analysis

The Morlet wavelet analysis method was used to analyze the primary periods of 63a area affected by flood, 58a area affected by drought, 44a area affected by hailstorms, and 40a area affected by low temperature events. Our findings indicate that wavelet contours of disaster have different intervals. According to wavelet analysis, there are several different scales of periods in the areas affected by disaster, and long periods contain short periods. Moreover, analysis shows that changes in the affected areas are superimposed by various oscillations, revealing that differences among the main periods and annual variations are significant.
Figure 4 is the isogram map of wavelet coefficient real number, the abscissa is the time (year), the ordinate is temporal scale. In this figure, the isogram curve is wavelet coefficient real, the real number is positive, the affected area is large, and the isogram curve is drawn with solid line. On the contrary, the real number is negative, the affected area is small, and the isogram curve is drawn with dotted line.
Figure 4 Wavelet coefficient of area affected by disasters

(a. Flood; b. Drought; c. Hailstorms; d. Low temperature)

Figure 4 shows that period oscillations of the areas affected by flood have gradually increased from the late 1980s, while those affected by drought, hailstorms and low temperatures have also gradually increased from 1990, 1994 and 1995, respectively.
The wavelet coefficient of area affected by flood revealed periodic changes in various time scales during different periods. Prior to 1990, there is a periodic change of a 5-28-year time scale, with strong and weak alternations of quasi twice oscillations. Three scales of periodic change - 8-15 years, 16-22 years, and 25-30 years - occurred in the late 1980s, with strong and weak alternations of quasi thrice oscillations appearing in a 8-15-year period, and a strong and weak alternation of quasi twice oscillations appearing in a 16-22-year period. Small scales of 3-7 years occurred after the 1990s.
Three kinds of periodic change (3-7 years, 8-14 years, and 16-22 years) of drought are widespread. Strong and weak alternations of quasi quartic oscillations appeared in 16-28 years period, and strong and weak substitutes of quasi sextic oscillations appeared in 8-14 years period. Oscillations gradually increased after 1980, and 3-7-year small-scale disturbances gradually strengthened.
Two dimensions of periodic change occurred in 10-15-year and 20-32-year scales, with the wavelet coefficient of area affected by hailstorms. Quasi twice oscillations in a 20-32-year and 10-15-year scale period showed quasi quintic oscillations, both gradually increasing after 2000. Moreover, the 5-10-year period superimposed on a 10-15-year period reduced to a 3-6-year small scale period after 1995.
The wavelet coefficient of area affected by low temperature shows that all types of period oscillations gradually strengthened after 1995. Specifically, the 11-24-year period increased after 1990, the 9-16-year period increased after 2000, and the 3-5-year small scale increased after 2005.
From the above analysis, we can see that the oscillation amplitudes of areas affected by all types of disasters have increased since the late 1980s, with small-scale disturbances in the late 1990s. Furthermore, the wavelet of drought indicates a strong oscillation across all scale periods. The information diffusion risk assessment shows that the surpass probability of drought is maximum, the recurrence interval is the shortest, and the growth rate of drought is likewise maximum (see Figure 2).

4.5 Correlation analysis

Amidst a backdrop of population expansion and rapid development of the economy, meteorological disasters show a clear growth trend into the 2000s. The influence of these disasters on agricultural production and socio-economic development has also increased, giving global warming a human face. By calculating the correlation coefficient between meteorology and agricultural indexes within the areas affected by weather-related disasters, from Table 5, we found that precipitation is the main meteorological factor of areas affected by flood, and that there is a significant positive correlation among temperature, drought and hailstorms. Cotton-cultivated areas have a strong positive correlation with areas affected by hailstorms, showing that hailstorms have a major impact on cotton. Meanwhile, there are negative correlations between food-cultivated areas and disaster affected areas, oil plant cultivated areas are positively correlated with floods and various other crop yields have a significant positive correlation with areas of disasters, especially hailstorms.
Table 5 Correlation coefficient of index and area affected by meteorological disasters in Xinjiang from 1961 to 2012
Area
affected		 1 2 3 4 5 6 7 8
Flood 0.571** 0.273 0.406** 0.116 0.397** 0.498** 0.235 0.276
Drought -0.05 0.416** 0.424** 0.365** 0.501** 0.451** 0.507** 0.472**
Wind
hailstorms		 0.382** 0.567** 0.605** 0.514** 0.658** 0.528** 0.693** 0.710**
Low
temperature		 0.049 0.409* 0.414* 0.416* 0.480** 0.409* 0.572** 0.557**
Area
affected		 9 10
11 12 13 14 12 13 14
Flood 0.197 -0.453** 0.301* 0.409** 0.454** 0.264 0.477**
Drought 0.492** -0.421** 0.531** 0.310* 0.462** 0.548** 0.510**
Wind
hailstorms		 0.697** -0.326** 0.647** 0.227 0.681** 0.652** 0.612**
Low
temperature		 0.563** -0.192 0.532** 0.114 0.434** 0.556** 0.414*

* Correlation is significant at the 0.01 level (2-tailed);* * Correlation is significant at the 0.05 level (2-tailed).

***1 is Precipitation, 2 is Mean annual temperature, 3 is Annual mean minimum temperature, 4 is Annual mean maximum temperature, 5 is Total population, 6 is Urban population, 7 is GDP, 8 is Gross output value of agriculture, 9 is Cultivated area, 10 is Yield, 11 is Crop, 12 is Food, 13 is Cotton, 14 is Oil plants.

5 Conclusions

(1) In analyzing floods, droughts, hailstorms, and low temperature disasters in Xinjiang from 1949 to 2012, a significant increasing trend was found. The growth slope of droughts was the sharpest, followed by low temperature events, hailstorms, and floods. The ratios covered by all disaster types acquired maximum volume from 2000 onwards. The spatial distribution maps of frequency revealed that the northern slope of Tianshan Mountains is a multiple disaster area, the southern slope of Tianshan is the area where more floods and hailstorms occur, and the west of Turpan-Hami Basin is the area where flood, drought and wind are prevalent.
(2) The surpass probability of disasters showed that when the ratio affected and ratio covered by all disaster types is 1%, the surpass probability is maximum and the recurrence interval is the shortest, at about 1-2 years. The risk sequence of drought risk is the largest, the second is hailstorms and low temperature, flood is the lowest. The surpass probability of drought is maximum, and the recurrence interval is the shortest. Due to the dry climate, scarce precipitation and high evaporation rates, when the ratio is affected by more than 10% of drought, the period is about once every two years. The water source of the oasis plains is mainly provided by precipitation in the mountains and snow melt water. Because there is less precipitation during the spring growing season, drought has the greatest effect on agricultural production. When the ratio affected by integrated disaster is from 10% to 20%, the recurrence interval is the shortest, at about 1-2 years. The surpass probability of the ratio affected by disaster is greater than the surpass probability of the ratio covered by disaster. Thus, it can be seen that the risk of wind is the largest. Some measures should be taken: (1) advocating water-conserving facilities, e.g., drop irrigation and spray irrigation; (2) promoting herdsmen to settle down and thus protect the natural grasslands and reduce the ranching loss caused by drought; (3) protecting the ecological environment and vegetation in areas where wind and hail disasters are prevalent, and meanwhile establishing and improving weather modification projects to reduce hails and increase precipitation.
(3) Wavelet analysis showed that the oscillation of drought periods has strengthened since 2000; the oscillation of flood periods have strengthened since the mid-1980s; the oscillation of hailstorms have strengthened since the mid-1990s; and the oscillation of low-temperature events have strengthened since 2005. The wavelet periods for all disaster types show strong oscillations after 2000, with the increase of small-scale period at the same time. Oscillations in drought are the strongest, followed by hailstorms, low temperature events, and floods.
Information diffusion model has limitations in using a single index to describe comprehensive risk. The affected area was as the index in information diffusion model, just assessment part of the vulnerability essentially. Information diffusion model needs to be combined with other methods to improve disaster assessment, including information diffusion method in the scenario simulation.
The increasing population and economic development in Xinjiang have led to expansion of human activity into desert areas, causing changes in land cover and water resources and damage to the ecological environment. Under climate change, the intensity and frequency of disasters have changed because of the frequent extreme climate events, thus human beings are facing more environmental disasters. By controlling population growth, along with rationally planning and utilizing water and land resources, and protecting and restoring the ecological environment, we can better deal with the uncertainty of future climate changes.

The authors have declared that no competing interests exist.

References

Publishing order | Descend order by publishing year | Descend order by cited within
1
Cao L X, Liu X Q, Zhang Let al., 2009. Temporal and spatial distribution characteristics and defensive countermeasures of hailstorm from 1998 to 2008 in Aksu.Desert and Oasis Meteorology, 3(2): 22-23. (in Chinese)

2
Chatman E A, 1986. Diffusion theory: A review and test of a conceptual model in information diffusion.J. Am. Soc. Inf. Sci. 37(6): 377-386.

3
Hu R J, Fan Z L, Wang Y J, 2001. Assessment about the impact of climate change on environment in Xinjiang since recent 50 years.Arid Land Geography, 24(2): 97-103. (in Chinese)

4
Hu R J, Ma H, Fan Z Let al., 2002. Response of water resources to climate change in Xinjiang.Journal of Natural Resources, 17(1): 22-27. (in Chinese)

5
Huang C F, 1997. Principle of information diffusion.Fuzzy Sets. Syst., 91(1): 69-90.

6
Huang C F, 2000. Demonstration of benefit of information distribution for probability estimation.Signal Process, 80(6): 1037-1048.

7
Huang C F, 2001. Information matrix and application.Int. J. Gen. Syst., 30(6): 603-622.

8
Huang C F, 2002a. An application of calculated fuzzy risk. Inf. Sci., 142(1): 37-56.

9
Huang C F, 2002b. Information diffusion techniques and small sample problem.Int. J. Inf. Technol. Decis. Mak., 1(2): 229-249.

10
Huang C F, Liu X L, Zhou G Xet al., 1998. Agricultural natural disaster risk assessment method according to the historic disaster data.Journal of Natural Disasters, 7(2): 1-4. (in Chinese)

11
IPCC, 2007. Climate Change: Impacts, Adaptation and Vulnerability: Working Group II Contribution to IPCC Fourth Assessment Report of the Intergovernmental Panel on Climate Change. London: Cambridge University Press.

12
James B E, James P K, Thomas H J, 2008. The increasing intensity of the strongest tropical cyclones.Nature, 455: 92-94.

13
Jiang F Q, Li Z, Hu R J, 2005a. Influences of drought on agriculture and disaster-chain effect during the second half of the 20th century in Xinjiang.Arid Land Geography, 28(4): 469-471. (in Chinese)

14
Jiang F Q, Zhu C, Mu G Jet al., 2005b. Magnification of flood disasters and its relation to regional precipitation and local human activities since the 1980s in Xinjiang, northwestern China.Natural Hazards, 36(3): 307-330.

15
Juraj M C, Taha B M J O, 2009. Trends in the timing and magnitude of floods in Canada.Journal of Hydrology, 375(3/4): 472-479.

16
Kerry E, 2005. Increasing destructiveness of tropical cyclones over the past 30 years.Nature, 436: 686-687.

17
Li B F, 2013. Study on the effects of climate change on water resources in the arid region of northwest China. Beijing: Dissertation of University of Chinese Academy of Sciences. (in Chinese)

18
Li Y, 2003. Change of river flood and disaster in Xinjiang during past 40 years.Journal of Glaciology and Geocryology, 25(3): 343-345. (in Chinese)

19
Liu X Z, Zhang A D, Li J Z, 2009. Geography Mathematics Method. Beijing: Science Press. (in Chinese)

20
Ma S H, 1994. Distribution of storm floods in Xinjiang.Bimonthly of Xinjiang Meteorology, 17(1): 25-26. (in Chinese)

21
Ma S H, Xi Y W, 1997. Some regularities of storm rainfall in Xinjiang, China.Acta Meteorologica Sinica, 55(2): 241-242. (in Chinese)

22
Mansur S, 2012. Analyzing the spatio-temporal variations of hailstorm disasters in southern Xinjiang region during recent 60 years.Journal of Glaciology and Geocryology, 34(4): 797-799. (in Chinese)

23
Mansur S, Lutubula Y, 2012. The characteristics of gale disaster and its impact on agricultural production in Southern Xinjiang in last 60 years.Agricultural Research in the Arid Areas, 30(1): 266-268. (in Chinese)

24
Parzen, 1962. On estimation of a probability density function and mode.Ann. Math. Statist., 33: 1065-1076.

25
Paul C D M, Wetherald R T, Dunne K Aet al., 2002. Increasing risk of great floods in a changing climate.Nature, 415: 515-516.

26
Peter J W, Holland G J, Curry J Aet al., 2005. Changes in tropical cyclone number, duration, and intensity in a warming environment.Science, 309: 1844-1845.

27
Shi Y F, Shen Y P, Hu R J, 2002. Preliminary study on signal, impact and foreground of climate shift from warm-dry to warm-humid in Northwest China.Journal of Glaciology and Geocryology, 24(3): 219-226. (in Chinese)

28
Sun G L, 2011. Spatio-temporal distribution of extreme hydrological events and response to climate change in Xinjiang. Beijing: Dissertation of Chinese Academy of Sciences. (in Chinese)

29
Wang Q X, Cui C X, Yao Y L, 2008. Variation trends and multi-scale analysis of flood affected area in various regions of Xinjiang.Acta Geographica Sinica, 63(7): 769-771. (in Chinese)

30
Wen K G, Shi Y G, 2006. Great Encyclopaedia of Meteorological Disasters of China: Xinjiang Volume. Beijing: China Meteorological Press. (in Chinese)

31
Wu S F, He W Q, Hu R Jet al., 2001. Analysis on the changing causes of the lakes in the basins and the plains in Xinjiang since recent years.Arid Land Geography, 24(2): 123-129. (in Chinese)

32
Xu G H, 1997. What does the global warming bring to the economic construction and sustainable development in Xinjiang?Bimonthly of Xinjiang Meteorology, 20(5): 1-3. (in Chinese)

33
Yang G M, Kong Q, Mao D Yet al., 2008. Analysis of the long lasting cryogenic freezing rain and snow weather in the beginning of 2008.Acta Meteorologica Sinica, 66(5): 837-839. (in Chinese)

34
Yang L, He L, 2005. Analysis on gale disaster degree in Xinjiang for 3 years and disaster zoning.Journal of Catastrophology, 20(4): 84-85. (in Chinese)

35
Yang Q, 1998. Characteristics of climate change in Xinjiang in recent 10 years.Bimonthly of Xinjiang Meteorology, 21(2): 11-12. (in Chinese)

36
Yang S Y, Li H H, Yan H Set al., 2012. Characteristics of extreme low temperature weather and the cause in the eastern Yunnan Province in 2011.Journal of Chengdu University of Information Technology, 27(1): 71-76. (in Chinese)

37
Zhang J L, Zhang L, 2011. Climate characteristics of severe hailstorm events during 50 years in Aksu, Xinjiang, China.Journal of Desert Research, 31(1): 237-238. (in Chinese)

38
Zhang X, Zhang C G, Wu J Xet al., 2009. Risk assessment of yield losses from agro-meteorological disasters in Fujian Province.Journal of Natural Disasters, 18(1): 1. (in Chinese)

Options
Outlines

/

〈 〉