EN中文

Journal of Geographical Sciences >

2014 , Vol. 24 >Issue 6: 980 - 992

DOI: https://doi.org/10.1007/s11442-014-1132-0

Research Articles

Influence of complex topography on global solar radiation in the Yangtze River Basin

  • WANG Li ,
  • QIU Xinfa ,
  • WANG Peifa ,
  • WANG Xiaoying ,
  • LIU Aili
Expand
  • School of Remote Sensing, Nanjing University of Information Science and Technology, Nanjing 210044, China

Wang Li (1979-), PhD Candidate and Lecturer, specialized in 3S integration and application in meteorology or hydrology. E-mail:

Received date: 2014-05-09

  Accepted date: 2014-08-10

  Online published: 2014-06-20

Supported by

National Natural Science Foundation of China, No.41175077.National Natural Science Foundation for Young Scholars, No.S0508016001.Guizhou Branch Major Projects [2011], No.6003

Copyright

Journal of Geographical Sciences, All Rights Reserved
Fold

Abstract

Global solar radiation (GSR) is the most direct source and form of global energy, and calculation of its quantity is highly complex due to influences of local topography and terrain inter-shielding. Digital elevation model (DEM) data as a representation of the complex terrain and multiplicity condition produces a series of topographic factors (e.g. slope, aspect, etc.). Based on 1 km resolution DEM data, meteorological observations and NOAA-AVHRR remote sensing data, a distributed model for the calculation of GSR over rugged terrain within the Yangtze River Basin has been developed. The overarching model permits calculation of astronomical solar radiation for rugged topography and comprises a distributed direct solar radiation model, a distributed diffuse radiation model and a distributed terrain reflectance radiation model. Using the developed model, a quantitative simulation of the GSR space distribution and visualization has been undertaken, with results subsequently analyzed with respect to locality and terrain. Analyses suggest that GSR magnitude is seasonally affected, while the degree of influence was found to increase in concurrence with increasing altitude. Moreover, GSR magnitude exhibited clear spatial variation with respect to the dominant local aspect; GSR values associated with the sunny southern slopes were significantly greater than those associated with shaded slopes. Error analysis indicates a mean absolute error of 12.983 MJm-2 and a mean relative error of 3.608%, while the results based on a site authentication procedure display an absolute error of 22.621 MJm-2 and a relative error of 4.626%.

Key words： rugged terrain; global solar radiation (GSR); distributed model; Digital Elevation Model; Yangtze River Basin

Cite this article

WANG Li , QIU Xinfa , WANG Peifa , WANG Xiaoying , LIU Aili . Influence of complex topography on global solar radiation in the Yangtze River Basin[J]. Journal of Geographical Sciences, 2014 , 24(6) : 980 -992 . DOI: 10.1007/s11442-014-1132-0

1 Introduction

Global solar radiation (GSR) is the most direct source of energy on Earth, thus affecting all physical, biological and chemical processes. GSR also represents a central component of the income radiation energy of the Earth’s surface radiation exchange; this is of primary significance with respect to the Earth’s surface radiation balance, air energy exchange and climate formation (Weng, 1997).
Moreover, GSR is also considered a key variable within global ecosystem modeling of carbon and nitrogen cycling, hydrological modeling and climate change prediction. Accordingly, significant national and international research efforts have focused on quantification of global surface radiation (Qiu, 2003). The development of remote sensing technologies has provided an important tool for the acquisition of quantitative solar radiation data on a regional scale; however, the majority of immediate remote sensing data can only reflect inversion solar radiation elements (Van Laake and Sanchez-Azofeifa, 2004; Tang et al., 2006). These include MODIS data and regional scale image data with high temporal resolution; daily solar radiation values (e.g. GMS data) typically have low spatial resolution, therefore, difficulties are frequently incurred in terms of national and international research requirements. Because of the inherent complexities and uncertainties associated with remote sensing inversion, solar radiation spatialization based on ground observation networks still represents an important data sourcing approach (He et al., 2004). Moreover, due to the high observational costs associated with solar radiation, observation density remains at a significantly lower level than that of routine meteorological stations; at present, solar radiation observatories number just over 1000 globally, of which more than 100 are located in China and are associated with shorter observational periods (Weng, 1997). Adequate description of solar radiation is extremely difficult based upon limited observational data; accordingly, the paucity of solar radiation data has represented a long-standing obstacle to accurate ecosystem process modeling. Spatialization of regional solar radiation values requires extrapolation and estimation based upon data collated from existing meteorological stations; to date, numerous solar radiation estimation models have been developed, which are typically divided into two categories, namely, theoretical and empirical models. Theoretical models aim to account for the primary atmospheric factors of solar shortwave radiation, and frequently comprise distinct simulations according to various radiation mechanisms, including both direct radiation and diffuse radiation. Factors typically include physical atmospheric factors (air molecules, aerosol dispersal, ozone, carbon dioxide and water vapor absorption) and meteorological factors (cloud cover, cloud type, cloud distribution and atmospheric water).
Myriad influential models utilizing a theoretical approach have been developed, for example, the Bird Clear Sky Model (Bird and Hulstrom, 1981), Iqbal Model C (Iqbal, 1983) and the MET-STAT (Meteorological/Statistical) Model, as employed in the construction of the American national solar radiation database (Maxwell, 1998). The Page Model has been applied for the development of the European solar radiation atlas (Page, 1997), while the ASHRAE Model is widely used in engineering and construction applications (American Society of Heating, 1999). The aforementioned theoretical models typically possess a solid physical foundation; however, they also necessitate complex model structures and numerous input parameters, including ozone thickness, aerosol content and atmospheric perceptible water. These parameters are difficult to obtain, thus preventing widespread model application in many cases. Conversely, empirical modeling employs a simpler approach and is frequently used in solar radiation climatology. Empirical modeling employs meteorological variables such as sunshine percentage and cloud cover, amongst others for the development of conventional estimation models, thus permitting regional scale solar radiation quantification.
The Yangtze River, with a total length of 6396 km, is the longest river in Asia and the third longest in the world; it originates from the Tibetan Plateau in Qinghai and flows through 11 provinces and cities before entering the East China Sea at Shanghai. Climate change is inherently related to surface water hydrology; accordingly, acquisition of sufficiently accurate and timely data is critical to appropriately assess the effects and evolution of climate change, anthropogenic activities and the ecological environment within the Yangtze River Basin, at varying temporal and spatial scales. Thus, the reliable quantification of solar radiation data in this region is of paramount importance.
Meteorological stations in China are typically situated in open flat locations characterized by an absence of natural shelter, with monitory data only representative of horizontal observational results within a limited radius. Therefore, solar radiation data collated at these stations are categorically horizontal observations. However, at regional scale, apart from cloudiness and other atmospheric variations, topography is the primary determining factor with respect to the distribution of incoming solar radiation (Aguilar et al., 2010). Variability in slope angle, slope orientation and shadows cast by topographic entities, can lead to significant local solar radiation gradients (Dozier, 1980; Dubayah, 1992; Dubayah, 1994; Dubayah and van Katwijk, 1992; Shi et al., 2013). Thus, accurate and direct description of the spatial distribution of GSR based solely on meteorological observations is difficult.
DEM data (1 km resolution) representing terrain conditions from 48 solar radiation observational stations within the Yangtze River Basin were employed to comprehensively account for the influence of solar radiation shielding. An estimation equation for the sunshine percentage and its relationship to GSR was subsequently developed to calculate an associated empirical coefficient. This was then used in concurrence with monthly solar radiation observations to obtain the spatial distribution of GSR within the Yangtze River Basin, in addition to the temporal and spatial distribution of climate change via utilization of sunshine percentage information from 1960 to 2010.

2 Data sources and processing

Meteorological data were collated and employed as follows: (1) monthly mean percentage of sunshine from 1960 to 2010 (MJm-2) within the Yangtze River Basin and 225 proximal meteorological stations; (2) daily GSR data from 48 solar radiation stations within the same spatial range (monthly mean sunshine percentage, monthly total radiation (MJm-2)); and (3) 1 km × 1 km resolution DEM data. Quality assurance analyses were undertaken on all employed data, including strict data screening, unit conversion for radiation data and data filtration. Overall, data from 227 sites were used to develop simulations (Figure 1).
Figure 1 Spatial distribution of meteorological stations associated with routine meteorological elements and solar radiation observation within and proximal to the Yangtze River Basin

3 Distributed GSR model for rugged terrain

3.1 Distributed GSR model for rugged terrain

Numerous previous studies have focused on estimation of solar radiation at the Earth’s surface (Steven, 1977; Temps and Coulsom, 1977; Iqbal, 1983; Proy et al., 1989; Dozier and Frew, 1990). If multiple reflections between the Earth’s surface and the atmosphere are not considered, surface solar radiation within regions characterized by complex terrain is composed of direct solar radiation, diffuse radiation and reflected radiation sky terrain, which is
where Qαβ denotes monthly GSR total within complex terrain (MJm-2), Qbαβ represents the monthly total of direct solar radiation within complex terrain (MJm-2), Qdαβ is the monthly total of diffuse solar radiation within complex terrain (MJm-2) and Qrαβ is the monthly total of terrain reflectance radiation (MJm-2).
3.1.1 Distributed direct solar radiation (DSR) model for rugged terrain
Based on the theory of DSR on slopes, the calculation formula of direct solar radiation (Qbαβ) in areas characterized by rugged terrain is:
where Q0αβ is the extraterrestrial solar radiation quantity associated with rugged terrain (Fu, 1958), Qbαβ is the DSR quantity associated with rugged terrain (Zeng et al., 2005a), Q0 is the extraterrestrial solar radiation quantity on a horizontal plane and Qb is the DSR quantity on a horizontal plane (Zuo et al., 1991).
Given Q0αβ, Q0 and Qb, the distribution of DSR quantity in areas characterized by rugged terrain Qbαβ may be quantified using equation (2). In the current study, Q0 and Q0αβ had been obtained using a previously developed algorithm (Zeng et al., 2003), with Qb simulated via statistical data-fitting models.
3.1.2 Distributed diffuse solar radiation model of rugged terrain
The underlying mechanism of diffuse solar radiation is relatively complex, thus creating difficulties with respect to accurate calculation of the quantity of diffuse radiation reaching the surface in areas with complex terrain (Weng, 1997). Existing diffuse radiation models of terrain slope are of two general types, namely, isotropic models (Liu and Jordan, 1962) and anisotropic models (Hay, 1979; Hay and McKay, 1985). Anisotropic models operate under the premise of anisotropic diffuse radiation intensity; the quantity of diffuse radiation reaching the surface in areas with complex terrain depends upon the degree of terrain masking V, in addition to other factors (Li et al., 1999; Zeng et al., 2003; Li and Weng, 1988; Rahoma, 2001; Lagib et al., 1999). The quantification of diffuse radiation, Qdαβ, in areas characterized by complex terrain is presented in equation (3). In the current study, modified anisotropic modeling has been employed:
where Qdαβ is the monthly total of diffuse radiation in complex terrain (MJm-2), Qd is the monthly total of horizontal diffuse radiation (MJm-2) and Rb is the ratio Qb/Q0.
3.1.3 Distributed terrain reflectance radiation model of rugged terrain
The terrain reflectance calculation model for solar shortwave radiation, Qrαβ, is presented in equation (4) (Zuhairy and Sayigh, 1995; Antonic, 1998):
where Qrαβ is the monthly quantity of terrain-reflected solar shortwave radiation (MJm-2), Q is the monthly quantity of horizontal GSR (MJm-2) and αs is the mean monthly surface albedo. Reference albedo is outlined in Section 3.4.

3.2 Horizontal DSR and diffuse radiation model

3.2.1 Horizontal GSR Q model
Several previous studies have reported a correlational relationship between GSR and sunshine percentage; accordingly, a linear estimation model (Kimball, 1919) has been employed as follows:
where aG and bG represent empirical coefficients affected by climactic characteristics (i.e. cloudiness), atmospheric transparency and other factors that have no direct relationship with terrain, s is the sunshine percentage (the percentage ratio of actual sunshine duration and astronomically possible sunshine duration) and kt = Q/Q0 is the clearness index.
Physically, equation (5) shows that when s = 0, Q → Q0aG and Q (value of incident surface light) is minimized; whereas, when s → 1, Q → Q0 (aG + bG) and Q is maximized.
Based on the fitted model in combination with the Q-linear form, the number of Q observational stations is more than that of Qb. In addition to temporal variation, spatial variation was also considered with respect to the empirical coefficient. Typically, four procedures are undertaken for Q fit modeling, as follows. (1) All meteorological observation stations for all months are amalgamated into a single sample dataset (Q) to establish a uniform Q estimation model (model N = 1). (2) All stations for the same months are amalgamated as a sample data set of Q for the development of Q estimate patterns by month (model N = 12). (3) Use of a single meteorological observation station for all months as a sample data set of Q followed by the development of Q estimation models by station (model N = 48). (4) Use of a single weather station in the same month as a sample data set of Q to develop estimate models by month and station (model N = 48 × 12 = 576). In the month-based model, temporal patterns empirical coefficients are considered, while spatial variation is accounted for via the station-based model. Accordingly, with respect to statistical estimation accuracy, resulting patterns from the aforementioned month-based and station-based models were used to obtain aG and bG. Via inverse distance weighting (IDW) interpolation on calculated aG, bG and s, the mode (equation 5) was used to calculate monthly Q.
3.2.2 Improved horizontal direct radiation and diffuse radiation component decomposition model
Direct radiation is the primary component of global radiation reaching the Earth’s surface, with direct radiation and GSR exhibiting a high level of correlation (Louche et al., 1991). Sunshine percentage and GSR are also closely related; thus, the association direct radiation and sunshine percentage may be directly calculated. Zeng et al. (2005b) have previously applied a modified calculation formula to the Yellow River basin, as follows:
where s is the sunshine percentage, a, b and c are empirical coefficients determined by the corresponding measured data and all other notations have been previously outlined.
Physically, equation (6) shows that when s = 0, there is no direct radiation and Qb = 0; when s → 1, GSR surface incidence is primarily composed of direct radiation, Qb → Q0 (aG + bG) (1-a). In the current study, equation (6) has been applied using just sunshine percentage (s) observations for the estimation of Qb.
Diffuse radiation is also an important quantitative component of GPS reaching the Earth’s surface. Based upon previous research pertaining to diffuse radiation model calculations (Liu and Jordan, 1963; Bartoli et al., 1982), a model for horizontal diffuse radiation Qd calculation takes the following form:
where Qd is the monthly quantity of horizontal diffuse radiation, and a, b, and c are experience coefficients required for determination of corresponding measured data.
Equation (7) shows that, when s=0, horizontal solar radiation is entirely composed of diffuse radiation; when s→1, horizontal solar radiation is primarily composed of direct radiation.
3.2.3 Horizontal solar radiation sunshine percentage calculation model
Sunshine percentage has been explained above. Possible sunshine duration may be directly calculated via a pre-existing astronomical equation, while actual sunshine duration may be obtained from meteorological observation. An IDW interpolation method has been used in the current study to derive the spatial distribution of sunshine percentage s within the scope of the Yangtze River Basin using data from the Yangtze River Basin and sunshine percentage data from 227 meteorological stations observations (Figure 1).

3.3 Distributed model of the degree of terrain masking

In complex terrain, mountain shelter depends upon the degree of mutual shading provided by the surrounding topographical features; numerical integration within a 2π orientation is required for accurate quantification of mutual shading. With respect to the undulating terrain of mountain P, the following distributed model algorithm pertaining to mountain has been developed (Qiu, 2003):
Along the circumference of the integral line (2π), mean mountain shade Vi is used to obtain mountain shade V. In equation (8), n pertains to a given azimuth integration step ΔΦ (degrees), with integration number and subsequent rounding along the 2π circumference.

3.4 Surface albedo calculation model

As an element of the surface shortwave radiation balance, surface albedo determines the distribution of energy between the ground surface and atmosphere via ground energy exchange; accordingly, it is a central parameter with respect to radiative transfer, numerical weather prediction and general circulation models (Zeng et al., 2003).
Surface albedo reflects the surface reflectance characteristics of solar radiation, thus, surface albedo variation has a significant impact on land surface processes. Surface albedo is frequently treated as a constant in traditional lumped evapotranspiration models for calculating shortwave radiation balances. However, it is a complex parameter, which may be affected by multiple variables including the angle of solar elevation, underlying surface roughness, soil moisture and vegetation type. Therefore, albedo data should reflect the spatial data distribution, with remote sensing representing a powerful tool in this regard.
The development of satellite remote sensing technology has permitted the collation and quantification of increasingly accurate ground albedo data; conventional climatology also represents a potential albedo data source, with both methods requiring subsequent inversion calculations (Xu and Liu, 2002; Arnfield, 1975; Morton, 1983). The inversion formula for albedo based on NOAA-AVHRR data is given by equation (9) (Valiente et al., 1995):
where αs is the mean monthly surface albedo, ρCH1 and ρCH2 are AVHRR channels 1 and 2 observations. Monthly observations from NOAA-AVHRR channels 1 and 2 (8 km × 8 km resolution) during the period 1981 to 2010 have been employed to obtain a monthly albedo spatial distribution for the Yangtze River Basin.

4 Distribution of GSR of complex terrain in the Yangtze River Basin

4.1 Spatial distribution of GSR of rugged terrain in the Yangtze River Basin

Based upon the spatial distribution of annual global radiation means for rugged terrain within the Yangtze River Basin (1960-2010) (Figure 2), GSR exhibits a ‘ladder-like’ distribution. The value of GSR associated with the Qinghai-Tibet Plateau (upriver), the Hengduan Mountains (southwest) and the western Sichuan Basin have the highest levels of GSR. Among these, the magnitude of annual solar radiation associated with the Tibetan Plateau occurs within the range of 6500-7247 MJm-2. A second GSR gradient is located in the Qinling-Daba Mountains in the northern Sichuan Basin, the southern Yunnan-Guizhou Plateau and the Southeast Hills in the middle-lower reaches of the river. Among which the annual magnitude of solar radiation of the Hengduan Mountains and the Yunnan-Guizhou Plateau occurs within the range of 5100-6400 MJm-2, while downriver areas of the Yangtze River in the hilly and plain region have a GSR range of 4000-5000 MJm-2, followed by the Sichuan Basin. The lowest GSR range is found within the Sichuan Basin (2700-3400 MJm-2). Overall, mean annual GSR is shown to positively correlate with altitude.
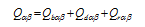
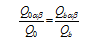
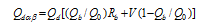
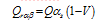
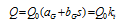
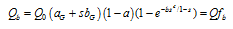
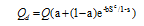
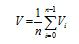
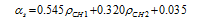
Figure 2 Spatial distribution of annual global radiation mean magnitude over rugged terrain within the Yangtze River Basin (1960-2010)
The spatial distribution of annual global radiation mean difference between rugged terrain and horizontal planes within the Yangtze River Basin (1960-2010) is presented in Figure 3. As shown, the magnitude of annual solar radiation differs significantly between rugged terrain and horizontal planes on both the sunny and shady sides of western mountains. These differences represent the composite effects of terrain-associated radiation factors. In characteristically flat areas, e.g. the Yangtze River Basin and Sichuan Basin, terrain-associated impacts may be ignored; however, in the Qinghai-Tibet Plateau and Hengduan Mountains, the impact of mountainous terrain is highly significant.
Figure 3 Spatial distribution of annual global radiation mean difference between rugged terrain and horizontal planes within the Yangtze River Basin (1960-2010)
The spatial distribution of seasonal global radiation mean over rugged terrain within the Yangtze River Basin (1960-2010) is presented in Figure 4. As shown, the magnitude of seasonal solar radiation may be ranked in the following order: summer > spring > autumn > winter, with the highest levels of radiation correlated with increasing altitude, e.g. the Tibetan Plateau, followed by the Hengduan Mountains and the Yunnan-Guizhou Plateau. The lowest levels of global radiation were associated with the Sichuan Basin. High radiation values during spring were found in the Tibetan Plateau and Hengduan Mountains, while radiation values during the summer months were high in the majority of investigated regions, except for Sichuan, Chongqing, etc. Radiation values during autumn within the Yangtze River source regions (e.g. Yushu) were relatively high, while other regions exhibited significantly lower values. The majority of regions exhibited low radiation values during winter months.
Figure 4 Spatial distribution of seasonal global radiation mean magnitude over rugged terrain within the Yangtze River Basin (1960-2010)

4.2 Local distribution of GSR over rugged terrain changing with topographical factors

The ratio of the monthly magnitude of terrain solar radiation and horizontal solar radiation (r = Qαβ / Q) represents the degree of impact on GSR accounted for by local topography. In the current study, spatial statistical analyses were conducted, based upon variation of the r curve with respect to season, latitude, altitude, slope and aspect. r curves were developed using calculated results of terrain GSR and horizontal GSR within the Yangtze River Basin, in concurrence with spatial analysis functions for altitude, slope and aspect. Accordingly, these analyses permit quantification of the influence of season, geographical latitude and terrain factors (like altitude, slope, aspect, etc.) on global radiation. r curve variation with respect to the Yangtze River Basin (1960-2010) is presented in Figure 5; for calculative purposes, spring, summer, autumn and winter were represented by April, July, October and January, respectively. Slope was defined as: 0°, northerly; 90°, easterly; 180°, southerly; 270°, westerly.
With respect to a latitude of 35° and a slope of 23° for varying seasons (Figure 5a), radiation variation during January exhibited the most dramatic response to aspect, followed by that of October, with the smallest response observed during July. Thus, it may be concluded that during autumn and winter months, solar radiation magnitude is most affected by aspect. From January onwards, with the aspect on the (horizontal) axis, solar radiation from a southern aspect (sunny) is significantly greater than 1, i.e. GSR of the topographic relief is greater than the horizontal plane, with the most significant differences observed in a southerly direction. Conversely, the solar radiation from a partially northern aspect (shady) is less than that observed from the horizontal plane, with the greatest difference located in a northerly direction. The trend curve for October was similar to that for January; however, the degree of influence (r) represented by aspect is weaker than that during January; in April, this influence is weaker again; in July, the influence exerted by the aspect becomes minimal, with an r value approaching 1, suggesting that GSR magnitude over the terrain is almost equal to that over the horizontal plane during this period. Moreover, r values of the westerly aspect and easterly aspect are both ≈1, indicating that GSR magnitude for both aspects are approximately equal. Additionally, local fluctuations in the graph line reflect mutual shadowing effects of topography.
Figure 5 Variation of r curve vs. slope of the Yangtze River Basin (1960-2010)
As the observed response for January was most significant, January has been used as a reference month for investigation of r-value variation with respect to slope, latitude and altitude.
As shown in Figure 5b, from 30°N to 36°N, in concurrence with increasing latitude, r significantly increases in parallel; the curves intersect at the eastern and western aspects, with respective r values of ≈1. From the western and eastern aspects to the southern aspect, the r value gradually increases, whereas a gradual decrease is observed within the transition from the western and eastern aspects to the northern aspect.
As shown in Figure 5c, the r value increases in concurrence with an increased degree of slope, as slope increases from 0° to 12°. This pattern is evident within the majority of curves, with an intersection of the eastern and western aspects, and an r value ≈1. The r value gradually increases during the transition from the western and eastern aspects to the southern aspect, whereas, the opposite is observed with respect to the transition from the western and eastern aspects to the northern aspect.
Local topography within the Yangtze River Basin is complex and comprises significant altitude variation. From Figure 5d, it is evident that with increasing height, the r value is affected by the degree of aspect, with this influence gradually increasing in parallel with altitude. Similarly, the intersections of the curves are located at the western and eastern aspects; transitions from the western and eastern aspects to the southern aspects concur with an increasing r value, while a decreasing r value is observed during the transition to the northerly aspect.
From Figure 5e, it may be observed that r values associated with the southern, southeastern, southwestern, western and eastern slopes are greater than or equal to 1, with increasing r values in concurrence with increasing slope, i.e. GSR magnitude is higher than that on horizontal terrain. The r values associated with the northern, northwestern and northeastern slopes are less than 1, with r values decreasing in parallel with increasing slope, i.e. GSR magnitude is lower than that on horizontal terrain.

4.3 Analysis of errors

Based on observational data from radiation stations during the period 1960-2010, mean monthly radiations from each station were calculated to obtain an overall simulation value for grid points via an adjacent similar pixels procedure. Through comparison of mean climate observations and simulation values, a mean absolute error of 12.983 MJm-2 was obtained, in concurrence with a mean relative error of 3.608% (Figure 6) (Qiu et al., 2009; Deng et al., 2013).
Figure 6 Contrast between observations and simulation values of normals of daily globa l radiation (1960-2010)

4.4 Site validation

To verify simulation accuracy, radiation stations not involved in the simulation process were employed to provide reference values. Simulation values for these sites were extracted from simulation results of the distributed GSR, and subsequently compared with the mean value of GSR based on observations from 1960 to 2010. Results indicate an absolute error of 22.621 MJm-2, in concurrence with a relative error of 4.626%.

5 Conclusions

Distributed simulation of GSR over rugged terrain is affected by interacting of astronomy, geography, local topography and other atmospheric factors. In the current study, astronomical radiation and terrain masking models have been developed for applications with respect to rugged terrain. Meteorological station observations from the Yangtze River Delta from 1960 to 2010, NOAA-AVHRR remote sensing data and 1 km × 1 km resolution DEM data were employed for the development of a DSR model, a terrain diffuse radiation model and a reflected radiation model. Comprehensive analyses of GSR results based upon characteristically rugged topography within the Yangtze River Basin were subsequently undertaken. The major study conclusions have been summarized as follows:
The use of topography astronomical radiation modeling and terrain masking modeling represents key technologies for the effective development of distributed topography DSR models, distributed topography diffuse radiation models and distributed topography reflection models.
Clustering procedures permit more stable and reliable empirical estimation of horizontal solar radiation. In the current study, data clustering procedures were based upon meteorological station and monitory month, and were used to examine the spatial and temporal properties of horizontal empirical coefficients. This approach was used to effectively overcome inherent instability with respect to empirical geo-statistical modeling over time and space. Accordingly, it provides a significantly enhanced approach for the quantitative spatial extension of GSR and others elements of ground space.
Results from the Yangtze River Basin indicate that GSR varies with season, altitude, latitude, slope and aspect. Aspect effects declined in concurrence with season in the order spring > winter > summer > autumn. Increased altitude, slope and latitude were shown to concur with an upward trend with respect to the degree of influence (r). The southern aspect (sunny) of GSR was shown to be significantly higher than the northern aspect (shaded).

The authors have declared that no competing interests exist.

References

Publishing order | Descend order by publishing year | Descend order by cited within
1
Aguilar C, Herrero J, Polo M J, 2010. Topographic effects on solar radiation distribution in mountainous watersheds and their influence on reference evapotranspiration estimates at watershed scale.Hydrology and Earth System Sciences, 14: 2479-2494.

2
American Society of Heating, 1999. Refrigerating and Air Conditioning Engineers (ASHRAE) Handbook: HVAC applications. Atlanta (GA): ASHRAE.

3
Antonic O, 1998. Modeling daily topographic solar radiation without site-specific hourly radiation data.Ecological Modeling, 113: 31-40.

4
Arnfield A J, 1975. A note on the diurnal, latitudinal and seasonal variation of surface reflection coefficient.Journal of Applied Meteorology, 14: 1603-1608.

5
Bartoli B, Cuorno V, Amato Uet al., 1982. Diffuse and beam components of daily global radiation in Geneva and Macerate.Solar Energy, 28(4): 307-311.

6
Bird R E, Hulstrom R L, 1981. A simplified clear sky model for the direct and diffuse isolation on horizontal surfaces. Golden, Colorado: US-SERI/TR-642-761, National Renewable Energy Laboratory.

7
Deng Yanjun, Qiu Xinfa, Zeng Yanet al., 2013. Comparison of horizontal global solar radiation models.Journal of the Meteorological Sciences, 33(4): 371-377. (in Chinese)

8
Dozier J, 1980. A clear-sky spectral solar radiation model for snow-covered mountainous terrain. Wat. Resour. Res. 16: 709-718.

9
Dozier J, Frew J, 1990. Rapid calculation of terrain parameters for radiation modeling from digital elevation data, IEEE Trans. Geosci. Remote Sens., GE-28, 963-969.

10
Dubayah R C, 1992. Estimating net solar radiation using Landsat Thematic Mapper and digital elevation data.Wat. Resour. Res., 28: 2469-2484.

11
Dubayah R C, 1994. Modeling a solar radiation topoclimatology for the Rio Grande river watershed. J. Veg. Sci., 5: 627-640.

12
Dubayah R, van Katwijk V, 1992. The topographic distribution of annual incoming solar radiation in the Rio Grande river basin. Geoph. Res. Let., 19: 2231-2234.

13
Fu Baopu, 1958. Influence of slope on sunshine and solar radiation. Journal of Nanjing University (Natural Science Edition), 2: 23-46. (in Chinese)

14
Hay J E, 1979. Calculation of monthly mean solar radiation for horizontal and inclined surfaces.Solar Energy, 23: 301-307.

15
Hay J E, McKay D C, 1985. Estimating solar radiance on inclined surfaces: A review and assessment of methodologies.Int. J. Solar Energy, 3: 203-240.

16
He Honglin, Yu Guirui, Liu Xinanet al., 2004. Study on spatialization technology of terrestrial eco-information in China (II): Solar radiation.Journal of Natural Resources, 19(5): 679-687. (in Chinese)

17
Iagib N A, Alvi S H, Mansell M G, 1999. Correlationships between clearness index and relative sunshine duration for Sudan.Renewable Energy, 17(4): 473-498.

18
Iqbal M, 1983. An Introduction to Solar Radiation. New York: Academic Press.

19
Kimball H H, 1919. Variations in the total and luminous solar radiation with geographical position in the United States. Mon. Weather Rev., 47: 769.

20
Li X, Cheng G D, Chen X Z, 1999. The improved solar radiation model on arbitrary terrain conditions. Chinese Science Bulletin, 44(9): 993-998. (in Chinese)

21
Li Z Q, Weng D M, 1988. Distribution characteristics and the computing model of the radiation scattering of slope.Meteorological Bulletin, 46(3): 349-356. (in Chinese)

22
Liu B Y, Jordan R C, 1962. Daily insulation on surfaces tilted towards the equator.Trans ASHRAE, 67: 526-541.

23
Liu B Y H, Jordan R C, 1963. The long-term average performance of flat-plate solar energy collections.Solar Energy, 7(2): 53-74.

24
Louche A, Notton G, Poggi Pet al., 1991. Correlation for direct normal and globe horizontal irradiation on a French Mediterranean site.Solar Energy, 46(4): 261-266.

25
Maxwell E L, 1998. METSTAT: The solar radiation model used in the production of the NSRDB.Solar Energy, 62(4): 263-279.

26
Morton F L, 1983. Operational estimates of areal evapotranspiration and their significance to the science and practice of hydrology.Journal of Hydrology, 66: 1-4.

27
Page J K, 1997.Proposed quality control procedures for the meteorological office data tapes relating to 642 761.

28
Proy C., Tanré D., Deschamps P. Y., 1989. Evaluation of topographic effects in remotely sensed data.Remote Sensing of Environment, 30: 21-32.

29
Qiu X F, 2003. Distributed modeling of solar radiation over rugged terrains [D]. Nanjing: Nanjing University. (in Chinese)

30
Qiu X F, Qiu Y P, Zeng Y, 2009. Distributed simulation of month mean temperature in Chongqing Mountain.Advances in Earth Science, 24(6): 621-628.

31
Rahoma U A, 2001. Clearness index estimation for spectral composition of direct and global radiations.Applied Energy, 68: 337-346.

32
Shi Guoping, Qiu Xinfa, Zeng Yan, 2013. Distributed modeling of three kinds of initial data for global solar radiation simulation in China.Scientia Geographica Sinica, 33(4): 385-392. (in Chinese)

33
Steven M D, 1977. Standard distributions of clear sky radiance.Quart. J. Roy. Meteor. Soc., 103: 457-465.

34
Tang B, Li Z L, Zhang R, 2006. A direct method for estimating net surface shortwave radiation from MODIS data.Remote Sensing of Environment, 103(1): 115-126.

35
Temps R C, Coulsom K L, 1977. Solar radiation incident upon slope of different orientations.Solar Energy, 19: 179-184.

36
Valiente J A, Nunez M, Lopez-Baeza Eet al., 1995. Narrow-band to broad-band conversion for Meteosat-visible channel and broad-band albedo using both AVHRR-1 and-2 channels.Int. J. Remote Sens., 16(6): 1147-1166.

37
Van Laake P E, Sanchez-Azofeifa G A, 2004. Simplified atmospheric radiative transfer modeling for estimating incident PAR using MODIS atmosphere products.Remote Sensing of Environment, 91(1): 98-113.

38
Weng D M, 1997. Studies on Radiation Climate of China. Beijing: China Meteorological Press. (in Chinese)

39
Xu X K, Liu S H, 2002. Deriving monthly means surface albedo.Meteorological Bulletin, 60(2): 216-219.

40
Zeng Y, Qiu X F, Liu C Met al., 2005a. Distributed modeling of direct solar radiation of rugged terrain over the Yellow River Basin.Acta Geographica Sinica, 60(4): 680-688. (in Chinese)

41
Zeng Y, Qiu X F, Liu S M, 2005b. Distributed modeling of extraterrestrial solar radiation over rugged terrains.Chinese Journal of Geophysics, 48(5): 1028-1033. (in Chinese)

42
Zeng Y, Qiu X F, Miao Q Let al., 2003. The spatial and temporal distribution of insolation duration over rugged terrains in our country.Progress in Natural Science, 13(5): 545-548. (in Chinese)

43
Zuhairy A A, Sayigh A A M, 1995. Simulation and modeling of solar radiation in Saudi Arabia.Renewable Energy, 6(2): 107-118.

44
Zuo D K, Zhou Y H, Xiang Y Q et al., 1991. On Surface Radiations. Beijing: Science Press.

Options
Outlines

/

〈 〉